5.1. Идентификация моделей динамических систем
Для выполнения качественного регулирования необходимы знания о динамическом поведении объекта управления. Процесс получения (синтеза) математического описания объекта на основе экспериментально полученных сигналов на его входе и выходе называется идентификацией объекта. Математическое описание может быть представлено в табличной форме или в форме уравнений. Идентификация может быть структурной, когда ищется структура математического описания объекта, или параметрической, когда для известной структуры находят величины параметров, входящих в уравнения модели. Когда ищутся параметры модели с известной структурой, то говорят об идентификации параметров модели, а не объекта.
Результатом идентификации может быть импульсная или переходная характеристика объекта, а также соответствующие им спектральные характеристики, которые представляются в виде таблицы (массива). Эти характеристики могут использоваться в дальнейшем для структурной и параметрической идентификации математической модели объекта регулирования или непосредственно для определения параметров ПИД-регулятора (как, например, в методе Зиглера-Никольса, см. раздел "Выбор параметров регулятора").
Несмотря на разнообразие и сложность реальных объектов управления, в ПИД-регуляторах используются, как правило, только две структуры математических моделей: модель первого порядка с задержкой и модель второго порядка с задержкой (см. раздел "Модели объектов управления"). Гораздо реже используются модели более высоких порядков, хотя они могут более точно соответствовать объекту. Существуют две причины, ограничивающие применение точных моделей. Первой из них является невозможность аналитического решения системы уравнений, описывающей ПИД регулятор с моделью высокого порядка (а именно аналитические решения получили наибольшее распространение в ПИД-регуляторах с автоматической настройкой). Вторая причина состоит в том, что при большом числе параметров и высоком уровне шума измерений количество информации, полученной в эксперименте, оказывается недостаточным для идентификации тонких особенностей поведения объекта. Это проявляется в плохой обусловленности системы линейных алгебраических уравнений, к которой приводит метод наименьших квадратов.
Выбор оптимальной модели обычно основан на компромиссе между качеством регулирования и сложностью модели. Для нелинейных процессов и при повышенных требованиях к качеству регулирования разрабатывают модели с индивидуальной структурой, основываясь на физике процессов, протекающих в объекте управления.
Если процесс любой сложности аппроксимировать моделью первого порядка с транспортной задержкой (рис. 5.1), то полученные таким способом постоянная времени  и задержка и задержка 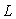 называются "эффективной постоянной времени" и "эффективной задержкой". называются "эффективной постоянной времени" и "эффективной задержкой".
Идентификация может выполняться с участием оператора, или в автоматическом режиме, а также непрерывно (в реальном времени) - в адаптивных регуляторах, либо по требованию оператора (в регуляторах с самонастройкой), подробнее см. раздел "Автоматическая настройка и адаптация".
Теория ПИД-регуляторов хорошо развита для линейных объектов управления. Однако практически все реальные объекты имеют нелинейность типа ограничения управляющего воздействия. Ограничение может быть связано, например, с ограниченной мощностью нагревателя при регулировании тепловых процессов, с ограничением площади сечения перепускного клапана, с ограничением скорости потока жидкости, и т. п. Ограничение "снизу" в тепловых системах связано с тем, что источник тепла не может, как правило, работать в режиме холодильника, когда этого требует закон регулирования.
Для минимизации нелинейных эффектов при идентификации объекта в рабочей точке ("в малом") используют малые изменения управляющего воздействия, когда нелинейности системы можно не учитывать.
Различают активную идентификацию (с помощью воздействия на систему, которое подается специально с целью идентификации) и пассивную - когда в качестве воздействий используют сигналы, имеющиеся в системе в процессе ее нормального функционирования. В пассивном эксперименте производят только наблюдение за поведением системы в нормальном режиме ее функционирования, пытаясь извлечь из этого наблюдения информацию, достаточную для настройки регулятора.
5.1.1. Модели объектов управления
Существует два способа получения модели объекта управления: формальный и физический. При формальном подходе используют модель типа "черный ящик", в которой не содержится информация о физических процессах, происходящих в объекте, или о его структуре. Синтез формальной модели сводится к выбору одной из небольшого числа моделей, описанных ниже, и идентификации ее параметров.
При физическом подходе модель объекта составляют в виде системы уравнений, описывающих физические процессы в объекте. При этом в качестве параметров модели могут использоваться геометрия объекта, физические параметры материала, фундаментальные физические константы. В физическую модель могут быть добавлены несколько формальных ("подстроечных") параметров, которые необходимо определить экспериментально из условия минимизации погрешности моделирования. Достоинством физических моделей является возможность установления аналитической зависимости между параметрами ПИД-регулятора и физическими параметрами объекта регулирования, например, зависимости постоянной интегрирования от количества яиц в инкубаторе или от количества жидкости в автоклаве. Другим достоинством физических моделей является то, что в процессе построения физической модели в нее вносится информация о структуре объекта. Наличие в модели информации о структуре объекта позволяет лучше отфильтровать помехи и возмущения в процессе подгонки модели к экспериментальным данным методом наименьших квадратов.
В отличие от физической, формальная модель справедлива только для того набора параметров, который был получен в процессе ее идентификации. При изменении параметров объекта (например, количества яиц в инкубаторе) идентификацию параметров модели нужно выполнять заново.
Модель первого порядка
Наиболее распространенными объектами управления являются системы, описываемые уравнениями тепломассопереноса. Реакция таких объектов (при условии, что они являются линейными по входному воздействию) на ступенчатое входное воздействие имеет задержку 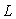 и точку перегиба рис. 5.1 - рис. 5.4. Точное решение этих уравнений осуществляется численными методами и в теории автоматического управления не используется. Используют достаточно простое выражение (модель первого порядка с транспортной задержкой) и точку перегиба рис. 5.1 - рис. 5.4. Точное решение этих уравнений осуществляется численными методами и в теории автоматического управления не используется. Используют достаточно простое выражение (модель первого порядка с транспортной задержкой)
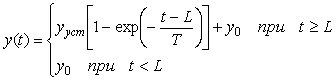 , , |
(5.1)
|
где 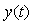 - выходная величина объекта регулирования (в данном случае - температура); - выходная величина объекта регулирования (в данном случае - температура); 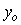 - значение выходной величины при - значение выходной величины при 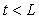 (см. рис. 5.1); (см. рис. 5.1);  - постоянная времени, - постоянная времени, 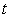 - время; - время; 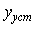 - установившееся значение выходной величины. На рис. 5.1 и рис. 5.2 кривая, построенная по выражению (5.1), показана штриховой линией. - установившееся значение выходной величины. На рис. 5.1 и рис. 5.2 кривая, построенная по выражению (5.1), показана штриховой линией.
Обычно при описании переходных процессов выходную переменную отсчитывают от постоянного уровня 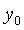 и нормируют на амплитуду входного скачка и нормируют на амплитуду входного скачка 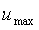 . Тогда величину . Тогда величину
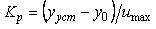 , , |
(5.2)
|
("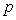 " - от слова "process") называют коэффициентом передачи объекта в установившемся режиме и уравнение (5.1) записывают в виде " - от слова "process") называют коэффициентом передачи объекта в установившемся режиме и уравнение (5.1) записывают в виде
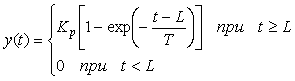 , , |
(5.3)
|
Временные характеристики очень сложно использовать при аналитическом анализе и синтезе ПИД-регуляторов. Для этих целей применяют их изображение по Лапласу или Фурье. Изображение по Лапласу переходной функции (5.3) имеет вид
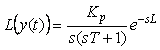 , , |
(5.4)
|
где 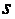 - комплексная частота, - комплексная частота, 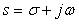 . Для передаточных функций обычно можно положить . Для передаточных функций обычно можно положить  и тогда и тогда 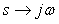 [Гроп]. Поскольку изображением входного ступенчатого воздействия является функция [Гроп]. Поскольку изображением входного ступенчатого воздействия является функция 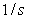 , то, поделив правую часть (5.4) на , то, поделив правую часть (5.4) на 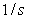 , получим реакцию объекта на единичный импульс (дельта-функцию Дирака), которую называют передаточной функцией объекта управления первого порядка с транспортной задержкой , получим реакцию объекта на единичный импульс (дельта-функцию Дирака), которую называют передаточной функцией объекта управления первого порядка с транспортной задержкой 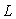 : :
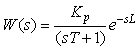 . . |
(5. 5)
|
Задержка выходной переменной 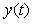 может быть двух видов: транспортной или обусловленной естественной инерционностью динамического объекта. Транспортная задержка входного воздействия может быть двух видов: транспортной или обусловленной естественной инерционностью динамического объекта. Транспортная задержка входного воздействия 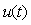 описывается выражением описывается выражением
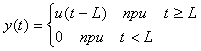 , , |
(5.6)
|
где 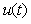 - входное воздействие на объект управления; - входное воздействие на объект управления; 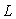 - длительность задержки. Изображение по Лапласу этого выражения имеет вид [Ротач] - длительность задержки. Изображение по Лапласу этого выражения имеет вид [Ротач]
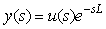 , , |
(5.7)
|
где 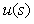 - изображение по Лапласу функции - изображение по Лапласу функции 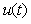 . .
Задержка, вызванная естественной инерционностью динамического объекта, точно моделируется дифференциальными уравнениями в частных производных и форма переходного процесса участка задержки является индивидуальной для каждого физического процесса, вызвавшего задержку. Приближенно такая задержка может быть смоделирована путем последовательного соединения нескольких звеньев первого порядка, однако это представление обычно неоправданно сложно. При синтезе ПИД-регуляторов, как правило, используется модель транспортной задержки, которая дает большую погрешность на начальном участке переходной характеристики (рис. 5.1), но является предельно простой. Если же важно получить точную форму колебаний в системе, то используют точные модели задержки.
Как видим, модель первого порядка описывается тремя параметрами: 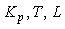 , которые должны быть найдены в процессе параметрической идентификации. , которые должны быть найдены в процессе параметрической идентификации.
Модель второго порядка
Если описанная модель первого порядка оказывается слишком грубой, используют модель второго порядка:
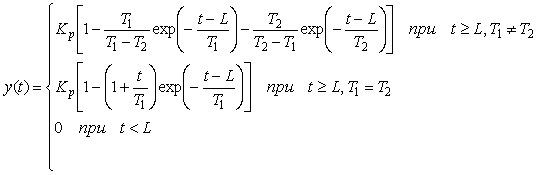 . . |
(5. 8)
|
Такая модель описывается четырьмя параметрами (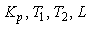 ), которые находятся методами идентификации, описанными ниже. Модель второго порядка имеет характерную точку перегиба на переходной характеристике (рис. 5.3 - рис. 5.4). ), которые находятся методами идентификации, описанными ниже. Модель второго порядка имеет характерную точку перегиба на переходной характеристике (рис. 5.3 - рис. 5.4).
Изображение по Лапласу импульсной характеристики модели второго порядка с задержкой имеет вид
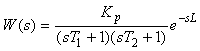 , , |
(5.9)
|
 |
 |
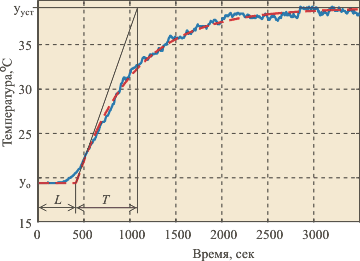
| Рис. 5.1. Температура трубы отопления здания после включения клапана подачи теплоносителя. Аппроксимировано моделью первого порядка. Измерено в RealLab! приборами серии "RealLab!" |
Рис. 5.2. Температура в помещении объемом 150 куб. м. после включения отопления (см. рис. 5.1). Аппроксимировано моделью первого порядка. Измерено в RealLab! приборами серии "RealLab!" |
 |
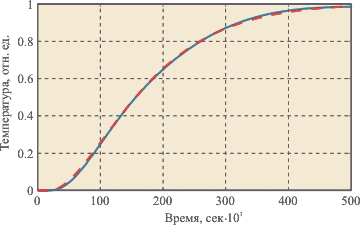 |
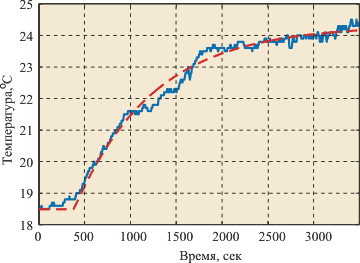
| Рис. 5.3. Переходная характеристика термошкафа "СНОЛ" при внешних возмущениях с большим временем корреляции. Аппроксимировано моделью второго порядка. Измерено в НИЛ АП приборами серии "RealLab!" |
Рис. 5.4. Переходная характеристика температуры в термошкафе при отсутствии шума и внешних возмущений. Аппроксимировано моделью второго порядка. Измерено в RealLab! приборами серии "RealLab!" |
На рис. 5.1 - рис. 5.5 приведены несколько переходных характеристик реальных объектов, снятых в производственном цехе с помощью модуля NL-4RTD, датчика ТСМ-50, ОРС сервера NLopc и программы MS Excel. Погрешность измерений составляет 1 градус, разрешающая способность - 0,01 градус. Экспериментально снятые точки (несколько тысяч) образуют на рисунках сплошную линию, кривая аппроксимирующей модели показана штриховой линией.
Модель в переменных состояния
Описанные модели первого и второго порядка довольно просты. Эта простота позволяет путем несложных графических построений определить их параметры, не прибегая к численным методам минимизации погрешности моделирования. Более точную модель можно получить, если использовать передаточную функцию, содержащую полином не только в знаменателе, но и в числителе. Однако такие модели слишком сложны для аналитического синтеза ПИД-регуляторов, поэтому они используются совместно с численными методами синтеза. При этом предпочтение отдается моделям в форме дифференциальных уравнений, а не в форме передаточных функций. Наиболее распространенной моделью в виде дифференциальных уравнений является система уравнений в переменных состояния.
Уравнения в переменных состояния имеют следующий вид:
где 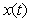 - вектор переменных состояния; - вектор переменных состояния; 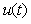 , , 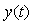 - векторы входных и выходных переменных объекта или скаляры для объекта с одним входом и одним выходом, - векторы входных и выходных переменных объекта или скаляры для объекта с одним входом и одним выходом, 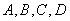 - матрицы постоянных коэффициентов, которые необходимо найти с помощью процедуры идентификации. - матрицы постоянных коэффициентов, которые необходимо найти с помощью процедуры идентификации.
Первое уравнение в (2.1) описывает динамику объекта, а второе (алгебраическое) связывает входные и выходные переменные с внутренними переменными объекта. Внутренние переменные получили название переменных состояния объекта.
Уравнения в переменных состояния могут быть преобразованы в форму передаточных функций и обратно.
В случае физических моделей переменные состояния отражают реальные переменные в объекте, например, температуру в некоторой точке внутри объекта. Однако чаще эти переменные не имеют физического смысла и служат только для формирования дифференциальных уравнений.
В качестве примера приведем матрицы, входящие в уравнение (5.10) для инкубатора "Птичка-100" (рис. 5.5) как объекта управления:
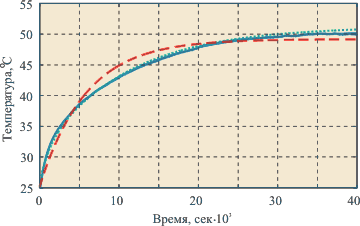
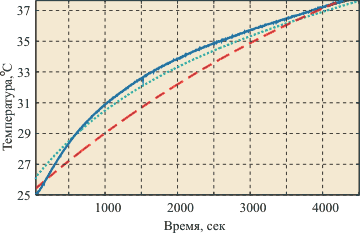
На рис. 5.5-а и рис. 5.5-б сплошной линией показана экспериментально полученная кривая; штриховой линией показана кривая, построенная по модели первого порядка, пунктирной линией - модель в переменных состояния (5.10) с матрицами (5.11); модель третьего порядка в переменных состояния практически сливается с экспериментальными данными. На рис. 5.5-б) показан в увеличенном масштабе начальный участок переходной характеристики.
Модель второго порядка в переменных состояния можно наглядно представить с помощью электрической цепи, показанной на рис. 5.6. В ней напряжения  и и 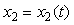 в узлах отображают состояние цепи в момент времени в узлах отображают состояние цепи в момент времени  и поэтому называются переменными состояния. Выходная величина и поэтому называются переменными состояния. Выходная величина 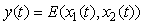 является алгебраической функцией от переменных состояния и, в более общем случае, от входного воздействия. является алгебраической функцией от переменных состояния и, в более общем случае, от входного воздействия.
 |
 |
|
а)
|
б) |
|
Рис. 5.5. Переходная характеристика температуры в серийном инкубаторе "Птичка-100" (а) и ее начальный участок в масштабе с увеличением (б). Штриховая линия соответствует модели 1-го порядка, пунктирная - 2-го, сплошная линия - 3-го и она сливается с экспериментальными данными. Измерено в RealLab! приборами серии "RealLab!"
|
С помощью преобразования Лапласа модель в переменных состояния можно преобразовать в модель в форме передаточных функций. В частности, для уравнений инкубатора ((2.1), (5.11)) получим
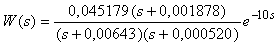 . .
Полагая 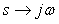 и переходя к показательной форме комплексной функции, получим амплитудно-частотную и фазо-частотную характеристики модели инкубатора, показанные на рис. 5.7. и переходя к показательной форме комплексной функции, получим амплитудно-частотную и фазо-частотную характеристики модели инкубатора, показанные на рис. 5.7.
Модели интегрирующих процессов
Выходная величина некоторых объектов управления при подаче на вход ступенчатого воздействия не стремится к установившемуся значению, как на рис. 5.1 - рис. 5.5-а продолжает изменяться в установившемся режиме. Такие переходные процессы называют интегрирующими. Пример интегрирующего процесса приведен на рис. 5.8. Это зависимость температуры в водонагревателе мощностью 2 кВт от времени после включения нагрева. Поскольку мощность нагревателя очень высока, вода успевает закипеть за время  . Это позволяет после разложения (5.3) в ряд Тейлора ограничиться первым членом ряда и тогда из (5.3) получим . Это позволяет после разложения (5.3) в ряд Тейлора ограничиться первым членом ряда и тогда из (5.3) получим
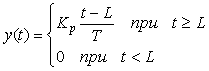 , , |
(5.12)
|
Передаточная функция такого процесса имеет вид
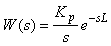 , , |
(5.13)
|
Другими примерами интегрирующих процессов могут быть: перемещение ленты транспортера; поворот оси двигателя, налив жидкости в емкость, рост давления в замкнутом сосуде.
Передаточные функции для интегрирующих процессов 1-го и 2-го порядка получаются из выражений (5.5) и (5.9) путем их умножения на изображение по Лапласу оператора интегрирования (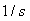 ): ):
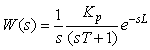 , , 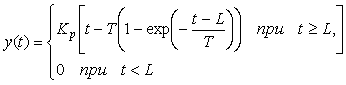 |
(5.14)
|
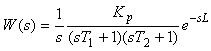 , , 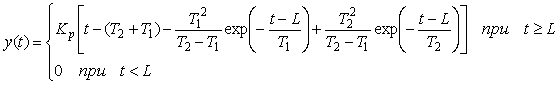 |
(5.15)
|
|
|
|
|
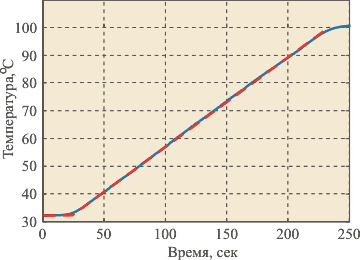
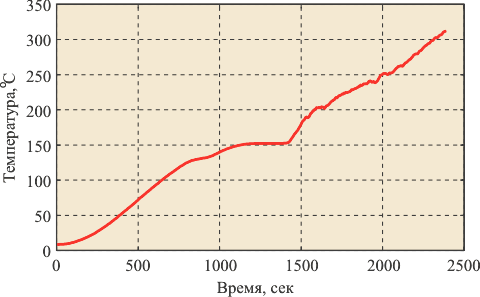
Рис. 5.8. Переходная характеристика чайника "Philips" с мощностью нагревателя 2 кВт: пример интегрирующего процесса первого порядка. Измерено в RealLab! приборами серии "RealLab!"
|
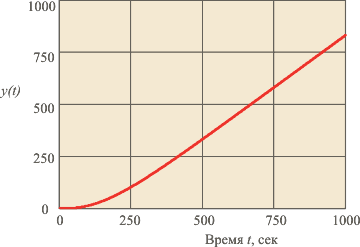
Рис. 5.9. Пример интегрирующего процесса второго порядка (5.15)
|
График функции (5.15), показан на рис. 5.9. В установившемся режиме, т.е. при  или при или при 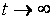 передаточная функция (5.15) вырождается в передаточная функция (5.15) вырождается в 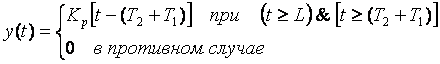 , а переходная функция - в , а переходная функция - в 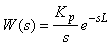 . .
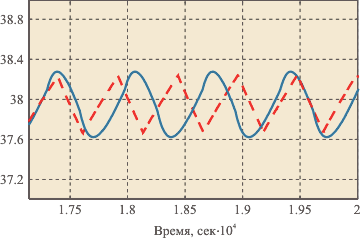
Отметим, что моделирование задержки с помощью сдвига функции на величину 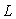 , как это сделано во всех приведенных моделях, дает удовлетворительные результаты для оценки устойчивости и качества регулирования, однако не позволяет получить даже качественно правильный результат при моделировании формы колебаний. В качестве иллюстрации на рис. 5.10 показаны процесс в инкубаторе, полученный с помощью модели третьего порядка с транспортной задержкой , как это сделано во всех приведенных моделях, дает удовлетворительные результаты для оценки устойчивости и качества регулирования, однако не позволяет получить даже качественно правильный результат при моделировании формы колебаний. В качестве иллюстрации на рис. 5.10 показаны процесс в инкубаторе, полученный с помощью модели третьего порядка с транспортной задержкой  (штриховая линия) и точное решение (сплошная линия). Несмотря на высокую точность модели (см. рис. 5.5-а), поведение системы качественно отличается от точного решения. Вопрос о выборе подходящей модели и ее точности не является тривиальным и зависит от цели моделирования. Обычно такой целью является получение заданного качества регулирования при заданном запасе устойчивости. (штриховая линия) и точное решение (сплошная линия). Несмотря на высокую точность модели (см. рис. 5.5-а), поведение системы качественно отличается от точного решения. Вопрос о выборе подходящей модели и ее точности не является тривиальным и зависит от цели моделирования. Обычно такой целью является получение заданного качества регулирования при заданном запасе устойчивости.
Приведенные выше модели не позволяют описать нелинейные физические процессы. Пример поведения нелинейного процесса иллюстрируется рис. 5.11, на котором показан график процесса разогрева металлического сплава, покрытого слоем глицерина. Резкое повышение теплоемкости в точке плавления сплава и в точке кипения глицерина являются причиной нелинейностей, которые можно наблюдать на рис. 5.11. Для описания таких процессов линейные модели можно использовать только на линейных участках характеристик.
|
|
|
|
Рис. 5.10. Форма колебаний в инкубаторе в режиме релейного регулирования при использовании модели третьего порядка с транспортной задержкой (штриховая линия) и точное решение (сплошная линия)
|
Рис. 5.11. Пример нелинейного процесса: разогрев легкоплавкого металлического сплава с глицерином на поверхности. Нелинейности по входному воздействию появляются в точке плавления сплава и в точке кипения глицерина. Измерено в RealLab! приборами серии "RealLab!"
|
Кроме описанных выше, существуют объекты с колебаниями во время переходного процесса (например, механические системы с упругими элементами), а также процессы, в которых выходная величина в начальный момент после включения начинает падать, а затем - расти, или наоборот. Такие процессы характерны для паровых котлов высокого давления (эффект "вскипания" поверхности [Ротач]).
Применение более сложных моделей позволяет улучшить качество регулирования, однако делает невозможным простой аналитический расчет параметров регулятора на основании параметров модели. Поэтому наибольшее распространение в ПИД-регуляторах нашли простейшие линейные модели первого и второго порядка.
Приведенные выше три типа моделей: в форме временных функций, в форме их изображений по Лапласу и в форме дифференциальных уравнений эквивалентны между собой и могут быть преобразованы одна в другую.
5.1.2. Выбор тестовых сигналов
|
|
|
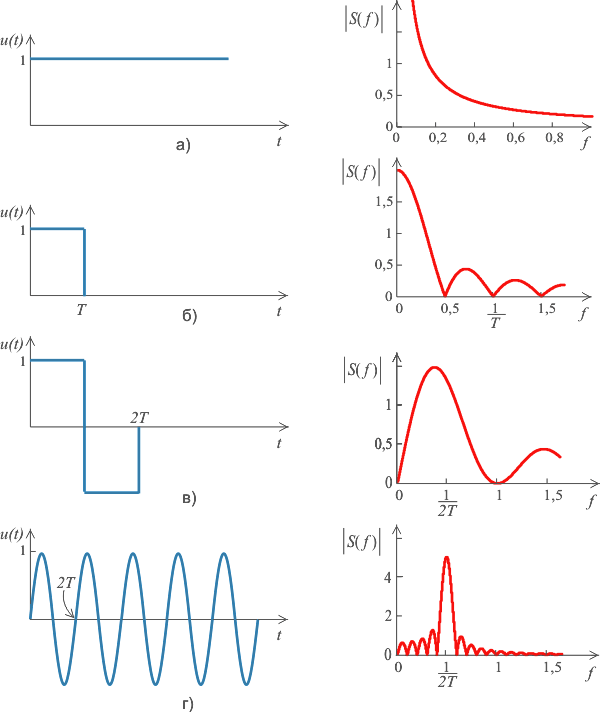
Рис. 5.12. Наиболее часто используемые тестовые сигналы. Слева - временные диаграммы, справа - модули спектральной плотности. Для сигнала г) взято 5 периодов синусоиды.
|
Для идентификации объекта управления необходимо измерять сигнал на его входе 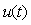 и реакцию и реакцию 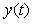 на выходе. Для идентификации в частотной области оперируют изображениями по Фурье входного на выходе. Для идентификации в частотной области оперируют изображениями по Фурье входного 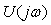 и выходного и выходного 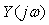 сигнала. Если входной сигнал подается специально с целью идентификации, то такой эксперимент называется активным. Если же идентификация выполняется путем измерения входных и выходных воздействий в системе в нормальном режиме ее функционирования, такой эксперимент называется пассивным. Идентификацию можно выполнить, подавая тестовый сигнал не только на вход системы, но и в виде изменения нагрузки (например, нагрузки на валу двигателя), а также параметров объекта (например, количества яиц в инкубаторе). сигнала. Если входной сигнал подается специально с целью идентификации, то такой эксперимент называется активным. Если же идентификация выполняется путем измерения входных и выходных воздействий в системе в нормальном режиме ее функционирования, такой эксперимент называется пассивным. Идентификацию можно выполнить, подавая тестовый сигнал не только на вход системы, но и в виде изменения нагрузки (например, нагрузки на валу двигателя), а также параметров объекта (например, количества яиц в инкубаторе).
Идентификация в пассивном эксперименте привлекательна тем, что не вносит погрешность в нормальное течение технологического процесса, однако ее достоверность крайне низка в принципе [Ротач] и может привести не к настройке, а расстройке ПИД-регулятора. Тем не менее, число патентов по ПИД-регуляторам с пассивной идентификацией равно числу патентов с активной идентификацией [Li].
При проведении активного эксперимента возникает задача выбора формы тестового воздействия. Используют сигналы в форме ступеньки (скачка), в форме прямоугольного импульса, линейно нарастающего сигнала, треугольного импульса, псевдослучайного двоичного сигнала (ПСДС) [Гроп], шума, отрезка синусоиды (частотный метод). Наиболее часто для настройки ПИД-регуляторов используют скачок (рис. 5.12-а), двойной прямоугольный импульс (рис. 5.12-в) и синусоидальный сигнал (рис. 5.12-г).
На рис. 5.12 справа приведены графики зависимости модулей спектральной плотности перечисленных сигналов от частоты (амплитудные характеристики спектра).
Тестовое воздействие должно иметь достаточно малую амплитуду, чтобы переходный процесс в объекте оставался в границах линейности. В то же время оно должно быть достаточно большим, чтобы увеличить отношение сигнала к шуму и внешним возмущениям. Перед подачей тестового воздействия объект должен находиться в установившемся состоянии и быть устойчивым.
Предположим, что в качестве тестового воздействия для идентификации мы выбрали синусоидальный сигнал (рис. 5.12-г. С увеличением количества периодов 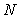 амплитуда боковых лепестков в спектре сигнала уменьшается, амплитуда основной гармоники увеличивается, ширина спектра сужается. При прохождении такого сигнала через объект управления на его выходе получается почти синусоидальный сигнал с той же частотой, что и на входе, изменяется только его амплитуда и фаза. Поэтому синусоидальный тестовый сигнал позволяет получить только одну точку на графике АЧХ или ФЧХ объекта, а для построения всей кривой необходимо подавать серию синусоидальных воздействий с разными частотами. амплитуда боковых лепестков в спектре сигнала уменьшается, амплитуда основной гармоники увеличивается, ширина спектра сужается. При прохождении такого сигнала через объект управления на его выходе получается почти синусоидальный сигнал с той же частотой, что и на входе, изменяется только его амплитуда и фаза. Поэтому синусоидальный тестовый сигнал позволяет получить только одну точку на графике АЧХ или ФЧХ объекта, а для построения всей кривой необходимо подавать серию синусоидальных воздействий с разными частотами.
Вместо этого можно использовать сигнал, спектральное разложение которого содержит множество гармонических составляющих. Такой сигнал можно подавать на объект идентификации однократно, но в результате получить информацию об объекте в широком диапазоне частот. Спектральную характеристику тестового сигнала необходимо выбирать такой формы, чтобы действующее значение сигнала в любом интервале частот многократно превышало соответствующую величину помехи. Граничная частота спектра тестового сигнала должна быть выше наибольшего по абсолютной величине полюса передаточной функции объекта [Справочник]. Точнее, выше, чем частота единичного усиления 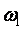 разомкнутого контура с обратной связью. До настройки регулятора, когда частота разомкнутого контура с обратной связью. До настройки регулятора, когда частота 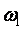 еще не известна, верхнюю граничную частоту спектра тестового сигнала выбирают выше частоты еще не известна, верхнюю граничную частоту спектра тестового сигнала выбирают выше частоты 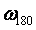 , на которой фазовый сдвиг выходного синусоидального сигнала объекта относительно входного составляет -180˚. Указанный диапазон частот важен потому, что именно на частоте , на которой фазовый сдвиг выходного синусоидального сигнала объекта относительно входного составляет -180˚. Указанный диапазон частот важен потому, что именно на частоте 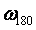 возникают колебания, когда объект находится на границе устойчивости в замкнутом контуре с релейным регулятором или П-регулятором. В контуре с ПИ-регулятором частота затухающих колебаний может быть ниже, и соответствовать точке, где сдвиг фаз в объекте составляет около -145˚ [Astrom] вследствие дополнительного фазового сдвига, вносимого интегратором. В ПИД-регуляторах дифференцирующее звено может скомпенсировать этот фазовый сдвиг и колебания возникнут на частоте возникают колебания, когда объект находится на границе устойчивости в замкнутом контуре с релейным регулятором или П-регулятором. В контуре с ПИ-регулятором частота затухающих колебаний может быть ниже, и соответствовать точке, где сдвиг фаз в объекте составляет около -145˚ [Astrom] вследствие дополнительного фазового сдвига, вносимого интегратором. В ПИД-регуляторах дифференцирующее звено может скомпенсировать этот фазовый сдвиг и колебания возникнут на частоте 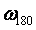 . .
Нижняя граница диапазона, в котором необходимо достаточно точно идентифицировать передаточную функцию объекта, должна быть примерно в 10 раз ниже частоты единичного усиления 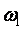 [Grassi]. Более точно нижнюю границу диапазона можно определить только после настройки ПИД-регулятора. [Grassi]. Более точно нижнюю границу диапазона можно определить только после настройки ПИД-регулятора.
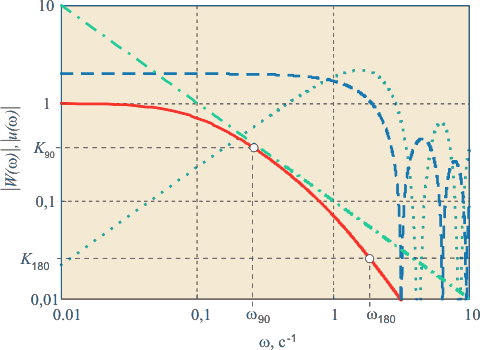
В качестве иллюстрации к сказанному на рис. 5.13, рис. 5.14 сплошной жирной линией показана амплитудно-частотная (АЧХ) и фазо-частотная характеристика (ФЧХ) объекта с передаточной функцией
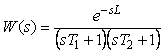 , , |
(5.16)
|
где 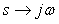 , , 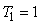 , , 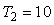 , , 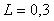 . Для получения хорошего отношения сигнал/шум амплитудная характеристика спектра тестового сигнала не должна иметь сильных провалов в интересующей области частот, чтобы обеспечить достаточно большое отношение сигнала к шуму. Этому условию, в частности удовлетворяют сигналы, показанные штриховой и пунктирной линиями на рис. 5.13. Желательно также, чтобы порядок функции, описывающей спектральную функцию тестового сигнала (т.е. порядок многочлена в знаменателе функции), был не ниже порядка объекта управления, поскольку крутизна спада АЧХ в области верхних частот увеличивается с ростом порядка. . Для получения хорошего отношения сигнал/шум амплитудная характеристика спектра тестового сигнала не должна иметь сильных провалов в интересующей области частот, чтобы обеспечить достаточно большое отношение сигнала к шуму. Этому условию, в частности удовлетворяют сигналы, показанные штриховой и пунктирной линиями на рис. 5.13. Желательно также, чтобы порядок функции, описывающей спектральную функцию тестового сигнала (т.е. порядок многочлена в знаменателе функции), был не ниже порядка объекта управления, поскольку крутизна спада АЧХ в области верхних частот увеличивается с ростом порядка.
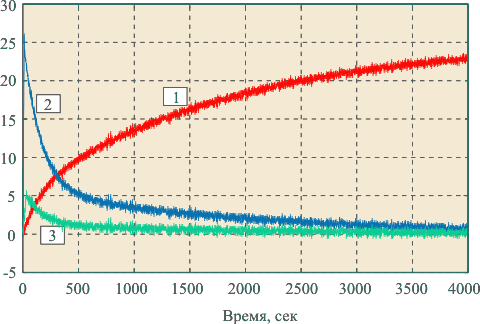
Ширина спектра и мощность тестового сигнала существенно влияют на точность идентификации. В общем случае более мощные и широкополосные сигналы позволяют определить большее число параметров передаточной функции. Данное утверждение иллюстрируется рис. 5.15, где кривые 2 и 3 представляют собой реакции на прямоугольные импульсы длительностью 60 сек и разной амплитуды. Из рисунка видно, что в формировании импульсной характеристики участвуют, по крайней мере, две ярко выраженные экспоненты с разыми постоянными времени, причем одна из них становится практически неразличимой (а ее параметры - неидентифицируемыми) на фоне помех при малой амплитуде тестового сигнала.
Невозможность идентификации части параметров объекта в условиях помех можно пояснить также с помощью рис. 5.6. При 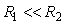 и и 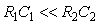 , , 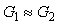 после подачи импульсного тестового сигнала после подачи импульсного тестового сигнала 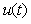 переменная переменная  будет расти очень медленно и за время, равное длительности тестового импульса, может остаться ниже уровня шума. Поэтому информация о ней будет отсутствовать в измерениях переменной будет расти очень медленно и за время, равное длительности тестового импульса, может остаться ниже уровня шума. Поэтому информация о ней будет отсутствовать в измерениях переменной 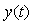 , следовательно, параметры , следовательно, параметры 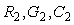 идентифицировать будет невозможно. Результатом идентификации в этом случае будет модель 1-го порядка, хотя объект имеет второй порядок. Для решения этой проблемы нужно увеличить амплитуду (при идентифицировать будет невозможно. Результатом идентификации в этом случае будет модель 1-го порядка, хотя объект имеет второй порядок. Для решения этой проблемы нужно увеличить амплитуду (при 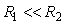 ) или длительность (при ) или длительность (при 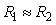 , , 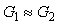 и и  ) тестового импульса. ) тестового импульса.
|
|

|
|
Рис. 5.13. АЧХ объекта 2-го порядка 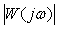 (сплошная линия) и амплитудная характеристика спектра различных тестовых воздействий (сплошная линия) и амплитудная характеристика спектра различных тестовых воздействий 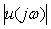 : прямоугольного импульса (штриховая линия); двойного импульса (пунктирная линия); скачка (штрихпунктирная) : прямоугольного импульса (штриховая линия); двойного импульса (пунктирная линия); скачка (штрихпунктирная)
|
Рис. 5.14. Фазо-частотная характеристика объекта управления 2-го порядка: штриховая линия - без транспортной задержки; сплошная линия - с задержкой.
|
Если идентификация выполняется без остановки технологического процесса (а это наиболее важный для практики случай), то могут существовать ограничения на максимальную мощность, длительность или энергию тестового сигнала, чтобы не нарушать нормальный ход технологического процесса. Например, в инкубаторе допускается подать импульс, кратковременно (на 5 мин.) повышающий температуру до 50˚С, однако повышение температуры даже на 1˚С в течение нескольких часов приводит к гибели зародыша. Поэтому возникает задача выбора тестового сигнала с требуемым спектром при ограничении на его мощность, длительность или энергию.
Наилучшую спектральную характеристику тестового сигнала можно получить, усложняя форму сигнала и увеличивая общее время идентификации. Для идентификации быстрых процессов (например, в электромеханических системах) получил широкое распространение псевдослучайный двоичный сигнал [Гроп], имеющий равномерный спектр в ограниченной полосе частот. Однако при управлении тепловыми процессами для ПИД-регуляторов наиболее критическим параметром является быстрота идентификации. Поэтому здесь чаще используют простые сигналы, которые, кроме быстроты идентификации, позволяют использовать простые расчеты по формулам вместо численных методов минимизации функционала ошибки. Конечно, достоверность результата при этом падает.
Даже тщательно выполненная идентификация может не дать положительного результата, если окажется, что объект существенно нелинеен (см. рис. 5.11). Для тестирования на линейность объект возбуждают серией тестовых воздействий разной амплитуды. Полученные реакции объекта нормируют на амплитуду тестового сигнала и сравнивают между собой. Для линейных объектов полученные кривые должны совпадать. Если различие между кривыми существенно превышает оценку погрешности идентификации, то объект следует рассматривать как нелинейный и использовать для него методы теории автоматического управления нелинейными системами.
После идентификации объекта разность между экспериментальными данными и расчетом по модели дает функцию погрешности идентификации, из которой после удаления систематической составляющей можно найти корреляционную функцию (или спектральную плотность мощности) шума измерений и внешних возмущений. Более точно идентифицировать шум и внешние возмущения можно путем измерения реакции объекта в рабочей точке при стабильном уровне входного воздействия.
В теории идентификации в качестве тестовых сигналов часто используют случайные сигналы. Суть метода заключается в том, что на вход объекта подают случайный стационарный тестовый сигнал 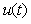 и измеряют реакцию на него и измеряют реакцию на него 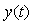 . Зная из эксперимента реализации случайных сигналов на входе и выходе объекта, находят оценки автокорреляционной функции входного сигнала и взаимной корреляционной функции между случайным сигналом на входе и выходе. Далее с помощью преобразования Фурье находят спектральные плотности мощности этих сигналов . Зная из эксперимента реализации случайных сигналов на входе и выходе объекта, находят оценки автокорреляционной функции входного сигнала и взаимной корреляционной функции между случайным сигналом на входе и выходе. Далее с помощью преобразования Фурье находят спектральные плотности мощности этих сигналов 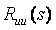 и и 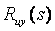 . После этого передаточная функция объекта управления . После этого передаточная функция объекта управления 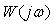 находится простым делением полученных Фурье-изображений: находится простым делением полученных Фурье-изображений:
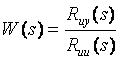 . . |
(5.17)
|
Используя обратное преобразование Фурье, можно найти импульсную характеристику объекта управления.
Однако на практике такой метод используют крайне редко, поскольку он требует накопления данных в течение времени, которое примерно в 100 раз превышает время взаимной корреляции шума между входом и выходом объекта [Справочник], что на практике займет неоправданно больше время для медленных (например, тепловых) процессов.
Единичный скачок
Единичный скачок (рис. 5.12-а и рис. 5.13, штрихпунктирная линия), в отличие от других тестовых сигналов, позволяет получить установившееся значение 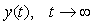 и точно найти коэффициент передачи объекта в установившемся режиме. Поэтому амплитуда скачка может быть выбрана гораздо меньшей, чем амплитуда прямоугольного импульса, что важно для процессов с нелинейностью типа ограничения (например, для тепловых процессов, как правило, это ограничение на мощность нагревателя). Однако длительность скачка, необходимая для достижения установившегося режима, может потребоваться слишком большой, неприемлемой для некоторых технологических процессов. и точно найти коэффициент передачи объекта в установившемся режиме. Поэтому амплитуда скачка может быть выбрана гораздо меньшей, чем амплитуда прямоугольного импульса, что важно для процессов с нелинейностью типа ограничения (например, для тепловых процессов, как правило, это ограничение на мощность нагревателя). Однако длительность скачка, необходимая для достижения установившегося режима, может потребоваться слишком большой, неприемлемой для некоторых технологических процессов.
График модуля спектральной плотности единичного скачка спадает со скоростью ‑20 дБ/дек, что делает проблематичным идентификацию самого интересного (начального) участка переходной характеристики (т. е. окрестности частоты 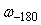 ) в условиях ограничения на энергию тестового сигнала. ) в условиях ограничения на энергию тестового сигнала.
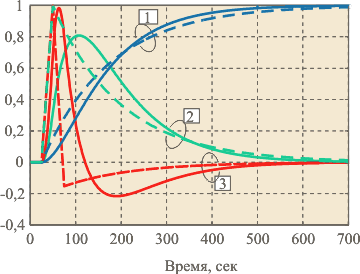
Реакции (отклики) объектов первого и второго порядка на единичный скачок отличаются незначительно (рис. 5.16, кривые 1). Это существенно увеличивает погрешность идентификации в условиях помех, поскольку относительная погрешность 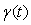 разности откликов объектов первого ( разности откликов объектов первого (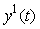 ) и второго ( ) и второго ( ) порядка быстро растет с уменьшением расстояния между ними ) порядка быстро растет с уменьшением расстояния между ними  : :
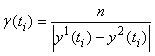 , , |
(5.18)
|
|
|
|
|
Рис. 5.15. Переходная (1) и импульсная (2, 3) характеристики инкубатора "Птичка-100" при наличии помех
|
Рис. 5.16. Реакция объектов 1-го (штриховая линия) и 2-го (сплошная линия) порядка на единичный скачок (1), на короткий прямоугольный импульс (2) и двойной прямоугольный импульс (3)
|
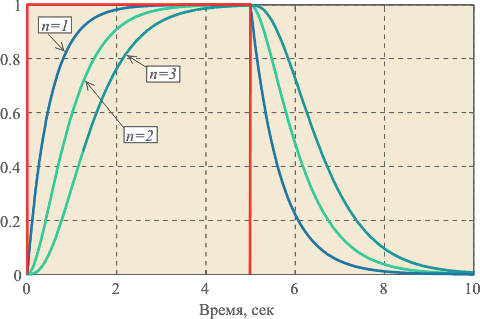
где 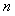 - среднеквадратическое напряжение помехи, - среднеквадратическое напряжение помехи, 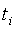 - момент времени для - момент времени для 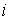 -того измеренного отсчета. Аналогичные погрешности для реакции на импульс и двойной импульс (рис. 5.16, кривые 2 и 3) гораздо меньше. -того измеренного отсчета. Аналогичные погрешности для реакции на импульс и двойной импульс (рис. 5.16, кривые 2 и 3) гораздо меньше.
С ростом порядка объекта различимость откликов моделей смежных порядков ухудшается. Это приводит не только к снижению отношения сигнал/шум, но и к ухудшению обусловленности системы линейных алгебраических уравнений, которую приходится решать при параметрической идентификации моделей высоких порядков методом наименьших квадратов.
Прямоугольный импульс
Прямоугольный импульс (рис. 5.12-б, -в и рис. 5.17 имеет большую спектральную плотность в области высоких частот, чем скачок (рис. 5.13, штриховая и пунктирная линии). При ограничении на энергию тестового сигнала это позволяет более точно выполнить идентификацию в наиболее важной высокочастотной области.
Вторым достоинством прямоугольного тестового импульса является большое различие в реакции объектов первого и более высоких порядков (рис. 5.16, кривые 2 и рис. 5.17), что позволяет улучшить идентифицируемость параметров моделей второго и более высоких порядков по сравнению с применением единичного скачка. После воздействия прямоугольного импульса система возвращается в первоначальное состояние, что уменьшает общее время эксперимента по сравнению с единичным скачком.
|
|
|
Рис. 5.17. Реакция на прямоугольный импульс объектов первого (1), второго (2) и третьего (3) порядка с передаточной функцией вида 
|
Прямоугольный импульс является приближенным аналогом единичного импульса (дельта-функции Дирака), которая имеет равномерную по частоте спектральную плотность. Поскольку единичный импульс физически нереализуем, используют его приближенный аналог - прямоугольный импульс максимально большой высоты и минимальной длительности. Высота импульса на практике всегда ограничена. Для тепловых процессов этой границей обычно является мощность нагревателя. При ограниченной высоте импульса его длительность будет определять отношение сигнал/шум на выходе объекта. Поэтому длительность импульса  (см. рис. 5.12-б выбирают по возможности большей, однако она должна быть меньше, чем (см. рис. 5.12-б выбирают по возможности большей, однако она должна быть меньше, чем 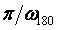 , чтобы наиболее интересная часть передаточной функции объекта была возбуждена равномерной частью спектра тестового сигнала (см. рис. 5.13, штриховая линия). , чтобы наиболее интересная часть передаточной функции объекта была возбуждена равномерной частью спектра тестового сигнала (см. рис. 5.13, штриховая линия).
Необходимость выбора большой высоты прямоугольного тестового импульса является его недостатком, который оказывается существенным при сильных помехах или резких технологических ограничениях на амплитуду входного воздействия.
Вторым недостатком прямоугольного импульса является невозможность точной оценки статического коэффициента передачи системы.
Разновидностью прямоугольного импульса является двойной прямоугольный импульс (рис. 5.12-в, который по сравнению с одиночным импульсом имеет двойной размах и максимум спектральной функции в области частоты 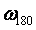 , что позволяет несколько повысить точность идентификации при тех же ограничениях на амплитуду импульса. , что позволяет несколько повысить точность идентификации при тех же ограничениях на амплитуду импульса.
Оба описанных тестовых сигнала позволяют выполнить аналитический расчет параметров модели объекта 1-го или 2-го порядка без применения численных методов оптимизации.
Отметим, что, несмотря на то, что импульсную характеристику системы (реакцию на единичный импульс) теоретически можно получить дифференцированием переходной характеристики (реакции на единичный скачок), дифференцирование экспериментально полученной кривой резко ухудшает отношение сигнала к шуму, поскольку оператор дифференцирования эквивалентен фильтру, выделяющему шумы из входных данных.
5.1.3. Частотная идентификация в режиме релейного регулирования
Идентификация с помощью широкополосных сигналов, к которым относятся единичный скачок и прямоугольный импульс, не позволяет получить достаточно достоверные результаты в условиях сильных шумов и жестких ограничений на энергию сигнала. Гораздо более высокую точность при малой амплитуде позволяет получить воздействие узкополосным сигналом, в качестве которого используют отрезок синусоидального сигнала (рис. 5.12-г). С ростом числа периодов сужается ширина спектра и растет спектральная плотность такого сигнала на частоте колебаний. Благодаря этому появляется возможность использовать узкополосный фильтр для выделения сигнала на фоне помех, что резко повышает достоверность идентификации. Однако при использовании фильтра перед измерением необходимо дождаться окончания переходного процесса, который тем длиннее, чем выше добротность фильтра. Это существенно увеличивает общее время на проведение экспериментов, тем более, что измерения выполняют для нескольких разных частот. Для ускорения процесса можно использовать тестовое воздействие в виде суммы гармонических колебаний с разными частотами, которые затем выделяют несколькими узкополосными фильтрами. Существенным недостатком этого метода является большое время идентификации. Поэтому его чаще используют только для измерения коэффициента передачи и фазового сдвига на частоте 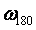 , а для идентификации других параметров объекта используют широкополосные тестовые сигналы. , а для идентификации других параметров объекта используют широкополосные тестовые сигналы.
Метод частотной идентификации в замкнутом контуре с релейным регулятором является самым распространенным в коммерческих ПИД-регуляторах с автонастройкой [Bertocco, Astrom, Cai]. Этот метод очень давно известен в микроэлектронике как метод кольцевого генератора. Он использует свойство замкнутой динамической системы с отрицательной обратной связью генерировать незатухающие колебания на частоте фазового сдвига -180˚ при петлевом усилении 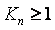 . .
Основная идея метода
Рассмотрим систему с отрицательной обратной связью, состоящую из релейного регулятора 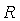 и объекта управления и объекта управления 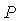 (рис. 5.18). Здесь регулятор (рис. 5.18). Здесь регулятор 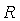 имеет два значения выходной величины имеет два значения выходной величины 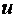 : :
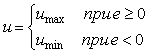 . . |
(5.19)
|
|

|
|
Рис. 5.18. Система с релейным регулятором в контуре регулирования для оценки параметров 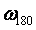 и и 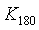
|
Гармонический сигнал, проходя через объект управления, изменяет свою амплитуду и фазу (рис. 5.13, рис. 5.14). Поскольку на входе объекта присутствует шум, в его спектре всегда найдутся такие гармонические составляющие с частотой 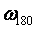 , которые, пройдя через объект управления, появятся на его выходе с той же частотой , которые, пройдя через объект управления, появятся на его выходе с той же частотой 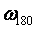 , но с отставанием по фазе на 180˚ от соответствующей входной составляющей. Если этот сигнал с выхода объекта опять подать на его вход с помощью отрицательной обратной связи, то общий фазовый сдвиг в петле с обратной связью составит уже 360˚, т. е. на частоте , но с отставанием по фазе на 180˚ от соответствующей входной составляющей. Если этот сигнал с выхода объекта опять подать на его вход с помощью отрицательной обратной связи, то общий фазовый сдвиг в петле с обратной связью составит уже 360˚, т. е. на частоте 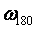 обратная связь в системе из отрицательной превращается в положительную. Это приводит к нарастанию циркулирующего по петле сигнала при петлевом усилении обратная связь в системе из отрицательной превращается в положительную. Это приводит к нарастанию циркулирующего по петле сигнала при петлевом усилении 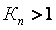 или его затуханию при или его затуханию при 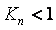 . Нарастание сигнала в некоторый момент начинает ограничиваться, например, нелинейностью типа насыщения, и тогда в системе устанавливаются стационарные колебания. При этом эффективный коэффициент усиления, найденный по первой гармонике колебаний на частоте . Нарастание сигнала в некоторый момент начинает ограничиваться, например, нелинейностью типа насыщения, и тогда в системе устанавливаются стационарные колебания. При этом эффективный коэффициент усиления, найденный по первой гармонике колебаний на частоте 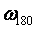 , становится равным единице: , становится равным единице: 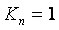 (т. к. после установления стационарных колебаний сигнал больше не усиливается). (т. к. после установления стационарных колебаний сигнал больше не усиливается).
Таким образом, в рассмотренной системе возникают незатухающие колебания, когда усиление по контуру с обратной связью (петлевое усиление) равно единице на частоте фазового сдвига в объекте 180˚. В нелинейной системе петлевое усиление на малом сигнале может быть больше единицы до момента, когда колебания установятся. В контуре регулирования с идеальным релейным регулятором (рис. 5.18) усиление до начала колебаний равно бесконечности. Поэтому колебания возникают всегда, если фазо-частотная характеристика включает в себя точку со сдвигом фазы 180˚.
Большинство объектов управления, не имеющих транспортной задержки, относятся к минимально-фазовым объектам, у которых существует однозначная связь между амплитудно-частотной и фазо-частотной характеристикой. Объект управления является минимально-фазовым, если его операторная передаточная функция не имеет нулей в правой полуплоскости комплексного переменного. В частности, минимально-фазовыми являются все описанные в п. "Модели объектов управления" модели, если у них транспортная задержка равна нулю.
|
|
|
|
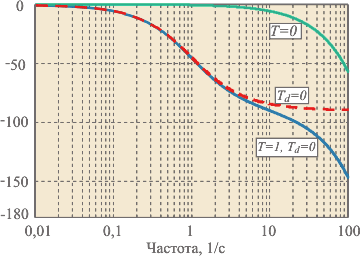
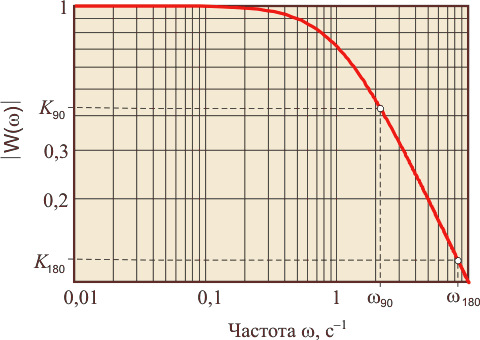
Рис. 5.19. Логарифмическая амплитудно-частотная характеристика объекта первого порядка, 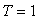 , , 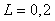
|
Рис. 5.20. Фазо-частотная характеристика объекта первого порядка без транспортной задержки (штриховая линия) и с ней (сплошная линия)
|
Обычно АЧХ строят в логарифмическом масштабе по обеим координатным осям и называют диаграммами Боде. При этом наклон линейных участков АЧХ измеряют в децибелах на декаду (дБ/дек). Например, объект первого порядка (5.5) имеет наклон АЧХ -20 дБ/дек (рис. 5.19) и при 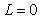 этому наклону взаимно однозначно соответствует максимальный фазовый сдвиг -90˚ при этому наклону взаимно однозначно соответствует максимальный фазовый сдвиг -90˚ при 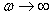 (рис. 5.20, пунктирная линия). Объект второго порядка (5.9) имеет наклон АЧХ -40 дБ/дек и ему соответствует максимальный фазовый сдвиг -180˚ при (рис. 5.20, пунктирная линия). Объект второго порядка (5.9) имеет наклон АЧХ -40 дБ/дек и ему соответствует максимальный фазовый сдвиг -180˚ при 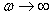 (рис. 5.13). Для объекта третьего порядка наклон АЧХ равен -60 дБ/дек и фазовый сдвиг -270˚. (рис. 5.13). Для объекта третьего порядка наклон АЧХ равен -60 дБ/дек и фазовый сдвиг -270˚.
Из изложенного следует, что система регулирования с объектом первого порядка без транспортной задержки всегда устойчива, даже в контуре с релейным регулятором. Система с объектом второго порядка может быть неустойчивой при 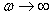 . Система с объектом третьего порядка и система любого порядка с транспортной задержкой в контуре с релейным регулятором всегда находится в режиме автоколебаний. . Система с объектом третьего порядка и система любого порядка с транспортной задержкой в контуре с релейным регулятором всегда находится в режиме автоколебаний.
Поэтому проектирование объекта управления нужно выполнять совместно с проектированием регулятора для него. Например, некоторые системы термостатирования используют нагревательный элемент в виде тонкой проволочки, через которую продувается воздух. Такая система имеет первый порядок передаточной функции и даже релейный регулятор для нее дает хорошее качество регулирования.
Система с объектом первого порядка перестает быть устойчивой, если в передаточную функцию добавляется транспортная задержка. При этом объект перестает быть минимально-фазовым и, несмотря на то, что наклон АЧХ остается равным -20 дБ/дек (рис. 5.19), в системе возникают колебания, поскольку фазовый сдвиг транспортной задержки  растет неограниченно с ростом частоты растет неограниченно с ростом частоты 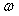 и на частоте и на частоте 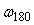 достигает -180˚ (рис. 5.20, сплошная линия). достигает -180˚ (рис. 5.20, сплошная линия).
|
|
|
|
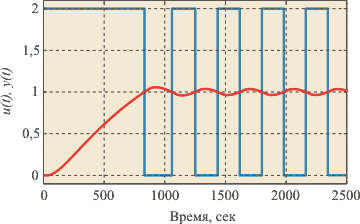
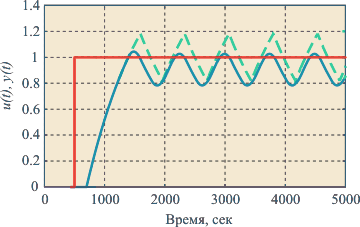
Рис. 5.21. Сигнал на входе (прямоугольные импульсы) объекта с передаточной функцией, показанной на рис. 5.13, рис. 5.14, и на его выходе (сплошная линия)
|
Рис. 5.22. Задающее воздействие (скачок) и форма сигнала на выходе замкнутой системы первого порядка в линейном режиме (сплошная линия) и с релейным регулятором (штриховая линия)
|
Поскольку в реальном объекте вследствие его пространственной протяженности всегда появляется (небольшая) транспортная задержка, в любой системе с релейным регулятором возникают колебания, однако их амплитуда на выходе объекта может быть пренебрежимо малой вследствие резкого снижения коэффициента передачи объекта с ростом частоты (см. рис. 5.19).
Таким образом, замкнутый контур с объектом управления и релейным регулятором позволяет найти частоту 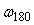 для объекта любого порядка, поскольку она равна частоте автоколебаний в такой системе. Найдем теперь коэффициент передачи объекта на этой частоте. К сожалению, его можно найти только приближенно, поскольку на вход объекта в системе с релейным регулятором воздействует последовательность прямоугольных импульсов, которая получается после прохождения сигнала обратной связи для объекта любого порядка, поскольку она равна частоте автоколебаний в такой системе. Найдем теперь коэффициент передачи объекта на этой частоте. К сожалению, его можно найти только приближенно, поскольку на вход объекта в системе с релейным регулятором воздействует последовательность прямоугольных импульсов, которая получается после прохождения сигнала обратной связи 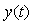 через релейный регулятор. Приближенный метод расчета основан на разложении входной последовательности прямоугольных импульсов в ряд Фурье с отбрасыванием всех гармоник, кроме первой. Возможность замены последовательности прямоугольных импульсов их первой гармоникой основана на том, что объекты с передаточными функциями вида (5.4) - (5.9) являются фильтрами, ослабляющими высшие гармоники. Поэтому серия прямоугольных импульсов, пройдя через такой объект, становится очень близкой к синусоидальному сигналу (рис. 5.21). Это позволяет считать, что после разложения входного сигнала в ряд Фурье через объект проходит только первая гармоника, а остальные подавляются. через релейный регулятор. Приближенный метод расчета основан на разложении входной последовательности прямоугольных импульсов в ряд Фурье с отбрасыванием всех гармоник, кроме первой. Возможность замены последовательности прямоугольных импульсов их первой гармоникой основана на том, что объекты с передаточными функциями вида (5.4) - (5.9) являются фильтрами, ослабляющими высшие гармоники. Поэтому серия прямоугольных импульсов, пройдя через такой объект, становится очень близкой к синусоидальному сигналу (рис. 5.21). Это позволяет считать, что после разложения входного сигнала в ряд Фурье через объект проходит только первая гармоника, а остальные подавляются.
Если размах прямоугольных импульсов на входе объекта равен 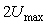 , то амплитуда первой гармоники этих импульсов, как известно из курса радиотехники, равна , то амплитуда первой гармоники этих импульсов, как известно из курса радиотехники, равна  . Если обозначить амплитуду первой гармоники сигнала на выходе объекта через . Если обозначить амплитуду первой гармоники сигнала на выходе объекта через 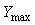 , то искомый коэффициент передачи системы на частоте , то искомый коэффициент передачи системы на частоте 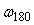 будет равен отношению амплитуды на выходе к амплитуде на входе: будет равен отношению амплитуды на выходе к амплитуде на входе:
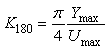 . . |
(5.20)
|
Пример. Рассмотрим АЧХ (рис. 5.13) и ФЧХ (рис. 5.14) объекта второго порядка вида (5.16). Из графика на рис. 5.14 можно найти частоту 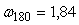 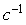 , а по рис. 5.13 - коэффициент передачи объекта на этой частоте , а по рис. 5.13 - коэффициент передачи объекта на этой частоте 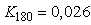 . Т. е. при включении такого объекта в контур с релейным регулятором получим колебания с частотой . Т. е. при включении такого объекта в контур с релейным регулятором получим колебания с частотой 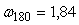 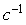 при усилении при усилении 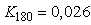 . .
Примерно эти же значения можно получить из эксперимента с релейным регулятором, по формуле (5.20), если из графиков на рис. 5.21 найти значения амплитуды на выходе 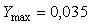 и входе и входе 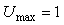 , а затем по формуле (5.20) рассчитать значение , а затем по формуле (5.20) рассчитать значение 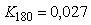 . Значение частоты . Значение частоты 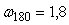 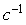 можно найти непосредственно по графику на рис. 5.21. Т.о., приближенная формула в данном случае дает достаточно низкую погрешность (около 4%). можно найти непосредственно по графику на рис. 5.21. Т.о., приближенная формула в данном случае дает достаточно низкую погрешность (около 4%).
Для объекта первого порядка с транспортной задержкой 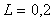 и постоянной времени и постоянной времени 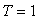 ( ( ) из рис. 5.20 можно найти ) из рис. 5.20 можно найти 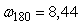 , из рис. 5.19 - , из рис. 5.19 - 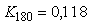 . Форма колебаний в системе с релейным регулятором показана на рис. 5.22, штриховая линия. Особенностью объекта первого порядка является существенное отличие формы колебаний от синусоидальной, что делает слишком грубым ее аппроксимацию первой гармоникой ряда Фурье, которая была использована при получении формулы (5.20). Для устранения этой проблемы вместо релейного регулятора можно использовать линейный усилитель, чтобы не искажать форму сигнала в системе. Тогда форма колебаний становится близкой к синусоидальной (рис. 5.22), сплошная линия. Такая колебательная система дает довольно точные значения . Форма колебаний в системе с релейным регулятором показана на рис. 5.22, штриховая линия. Особенностью объекта первого порядка является существенное отличие формы колебаний от синусоидальной, что делает слишком грубым ее аппроксимацию первой гармоникой ряда Фурье, которая была использована при получении формулы (5.20). Для устранения этой проблемы вместо релейного регулятора можно использовать линейный усилитель, чтобы не искажать форму сигнала в системе. Тогда форма колебаний становится близкой к синусоидальной (рис. 5.22), сплошная линия. Такая колебательная система дает довольно точные значения  и и 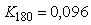 . Однако для обеспечения режима, близкого к линейному, петлевое усиление должно быть равно 1, т.е. усилитель должен обеспечит усиление в . Однако для обеспечения режима, близкого к линейному, петлевое усиление должно быть равно 1, т.е. усилитель должен обеспечит усиление в 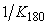 раз, где параметр раз, где параметр 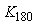 априори неизвестен. Это является основным недостатком метода колебаний в линейном режиме. априори неизвестен. Это является основным недостатком метода колебаний в линейном режиме.
Важным условием, которое нужно соблюдать при использовании идентификации в режиме релейного регулирования, является симметричность уровней 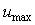 и и 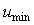 относительно уровня сигнала относительно уровня сигнала  , при котором , при котором 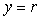 (см. рис. 5.18), т.е. должно выполняться условие (см. рис. 5.18), т.е. должно выполняться условие 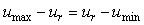 . В противном случае скорости нарастания сигнала выше уставки и спада ниже нее будут сильно различаться, а форма колебаний в системе будет существенно отличаться от синусоидальной (рис. 5.23), что приведет к высокой погрешности данного метода. . В противном случае скорости нарастания сигнала выше уставки и спада ниже нее будут сильно различаться, а форма колебаний в системе будет существенно отличаться от синусоидальной (рис. 5.23), что приведет к высокой погрешности данного метода.
Аналогичный эффект искажения формы колебаний возникает и в системах более высокого порядка, если транспортная задержка превышает наибольшую постоянную времени. С ростом задержки колебания становятся сначала треугольными, затем приближаются к трапецеидальным и прямоугольным. Это объясняется тем, что с ростом транспортной задержки реакция объекта на каждый из фронтов сигнала на выходе реле приближается к форме реакции на функцию единичного скачка (рис. 5.17). В частотной области указанный эффект объясняется тем, что с ростом задержки точка 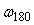 на рис. 5.19 и рис. 5.20) смещается влево, т.е. фильтрующие свойства объекта ухудшаются и он транслирует прямоугольный входной сигнал на свой выход с меньшими искажениями. на рис. 5.19 и рис. 5.20) смещается влево, т.е. фильтрующие свойства объекта ухудшаются и он транслирует прямоугольный входной сигнал на свой выход с меньшими искажениями.
|
|
|
Рис. 5.25. Ложные переключения реле вследствие шума
|
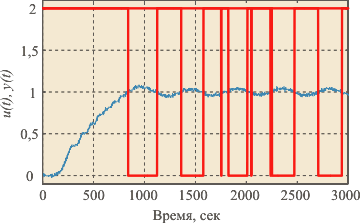
Для иллюстрации высокой разрешающей способности описанного метода на рис. 5.24 приведены процессы в двух моделях, у которых переходные характеристики различаются слабо, однако частоты колебаний в контуре с релейным регулятором отличаются в 4 раза. Благодаря узкой полосе сигнала он может быть эффективно выделен на фоне шумов (рис. 5.25), например, методом наименьших квадратов.
Описанный метод частотной идентификации позволяют получить только одну точку передаточной функции объекта, т.е. два параметра, которых недостаточно для нахождения трех параметров ПИД-регулятора. Поэтому используют дополнительное соотношение 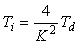 (см. п.5.6.3), которое позволяет найти третий параметр. (см. п.5.6.3), которое позволяет найти третий параметр.
Чтобы получить и другие точки АЧХ, используют реле с гистерезисом или фильтры, сдвигающие точку 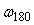 в сторону более низких частот. в сторону более низких частот.
Рассмотрим эти методы подробнее.
Изменение частоты колебаний с помощью интегратора
Для того чтобы в системе с релейным регулятором возникли колебания на частоте, существенно отличающейся от 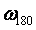 , в нее можно ввести интегратор (рис. 5.26) [Wei], который имеет передаточную функцию , в нее можно ввести интегратор (рис. 5.26) [Wei], который имеет передаточную функцию 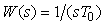 , где , где 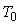 - произвольный нормировочный множитель. На рис. 5.26 после интегратора показан линейный ограничитель, отражающий наличие ограничений на входной сигнал объекта. Желательно выбирать - произвольный нормировочный множитель. На рис. 5.26 после интегратора показан линейный ограничитель, отражающий наличие ограничений на входной сигнал объекта. Желательно выбирать 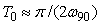 , тогда размах колебаний треугольной формы на выходе интегратора будет точно равен размаху прямоугольных импульсов на выходе реле. Однако, поскольку частота , тогда размах колебаний треугольной формы на выходе интегратора будет точно равен размаху прямоугольных импульсов на выходе реле. Однако, поскольку частота 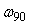 априори неизвестна, а выбор априори неизвестна, а выбор  влияет только на амплитуду колебаний в системе, величину влияет только на амплитуду колебаний в системе, величину 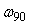 можно выбирать примерно в несколько (3...10) раз ниже ранее найденной частоты можно выбирать примерно в несколько (3...10) раз ниже ранее найденной частоты 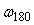 . Чем больше транспортная задержка . Чем больше транспортная задержка 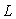 , тем меньше будет расстояние между точками , тем меньше будет расстояние между точками 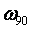 и и 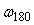 . .
|

|
|
Рис. 5.26. Система с релейным регулятором и интегратором для оценки параметров 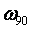 и и 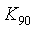
|
Модуль передаточной функции интегратора имеет наклон - 20 дБ на декаду, а фазовый сдвиг не зависит от частоты и равен -90˚. Поэтому колебания в системе возникают на частоте 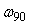 (рис. 5.14, рис. 5.20), когда сдвиг фаз в объекте управления составит -90˚ (поскольку суммарный сдвиг в интеграторе и объекте составит -180˚). Получив из эксперимента частоту (рис. 5.14, рис. 5.20), когда сдвиг фаз в объекте управления составит -90˚ (поскольку суммарный сдвиг в интеграторе и объекте составит -180˚). Получив из эксперимента частоту 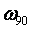 , можно найти модуль передаточной функции , можно найти модуль передаточной функции 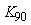 на этой частоте по той же формуле (5.20), что и для на этой частоте по той же формуле (5.20), что и для 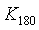 . Однако точность расчета можно повысить, если воспользоваться тем, что на выходе интегратора получаются треугольные импульсы, для которых легко найти амплитуду первой гармоники ряда Фурье . Однако точность расчета можно повысить, если воспользоваться тем, что на выходе интегратора получаются треугольные импульсы, для которых легко найти амплитуду первой гармоники ряда Фурье 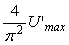 , где , где 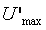 - половина размаха треугольных импульсов. Интегрируя сигнал, поступающий на входе интегратора, можно получить, что - половина размаха треугольных импульсов. Интегрируя сигнал, поступающий на входе интегратора, можно получить, что 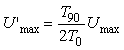 , где , где 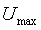 - половина размаха прямоугольных импульсов на выходе реле, - половина размаха прямоугольных импульсов на выходе реле, 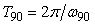 . Поэтому амплитуда первой гармоники сигнала на входе объекта будет равна . Поэтому амплитуда первой гармоники сигнала на входе объекта будет равна 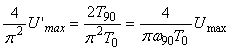 , откуда коэффициент передачи объекта на частоте , откуда коэффициент передачи объекта на частоте 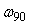 можно найти в виде можно найти в виде
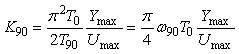 , , |
(5.22)
|
где 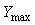 и и 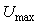 имеют тот же смысл, что и в (5.19). имеют тот же смысл, что и в (5.19).
Формула (5.22) дает довольно точные результаты. Для системы 2-порядка (5.16) расчет по формуле (5.22) на основании данных, полученных при моделировании системы, дает значения 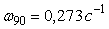 , , 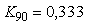 , а точный расчет дает , а точный расчет дает 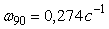 , , 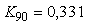 . Для системы 1-го порядка (рис. 5.19, рис. 5.20) расчет по формуле (5.22) дает . Для системы 1-го порядка (рис. 5.19, рис. 5.20) расчет по формуле (5.22) дает  , , 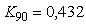 при точных значениях при точных значениях  и и 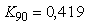 , а расчет по более грубой формуле (5.20) дает , а расчет по более грубой формуле (5.20) дает 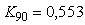 . .
Изменение частоты колебаний с помощью генератора
Для исключения погрешности формулы (5.20), связанной с усечением ряда Фурье, в работе [Wang] предлагается вместо интегратора на рис. 5.26 использовать генератор синусоидальных колебаний с амплитудой, равной амплитуде первой гармоники прямоугольных импульсов на входе реле:
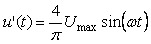 , , |
(5.23)
|
где 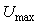 - половина размаха колебаний на выходе реле, - половина размаха колебаний на выходе реле, 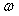 - частота колебаний в системе. Поскольку частота - частота колебаний в системе. Поскольку частота 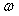 априори неизвестна, ее определяют итерационным путем. Сначала убирают из системы генератор (5.23) и находят частоту колебаний в нулевом приближении. Для этого используют 2...3 периода колебаний в системе. Затем полученное значение частоты подставляют в формулу (5.23) и находят колебания в системе с генератором. Полученное значение частоты опять подставляют в формулу (5.23). Несколько таких итераций позволяют получить точное значение частоты. априори неизвестна, ее определяют итерационным путем. Сначала убирают из системы генератор (5.23) и находят частоту колебаний в нулевом приближении. Для этого используют 2...3 периода колебаний в системе. Затем полученное значение частоты подставляют в формулу (5.23) и находят колебания в системе с генератором. Полученное значение частоты опять подставляют в формулу (5.23). Несколько таких итераций позволяют получить точное значение частоты.
Изменение частоты колебаний с помощью гистерезиса
Если в системе на рис. 5.26 использовать реле с гистерезисом, то частоту колебаний можно понизить. Объясняется это тем, что при подаче сигнала на вход реле с симметричным относительно нуля гистерезисом шириной 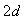 на выходе реле появляется сигнал с задержкой на выходе реле появляется сигнал с задержкой 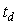 , обусловленной тем, что для срабатывания реле синусоидальный сигнал на входе должен достичь уровня , обусловленной тем, что для срабатывания реле синусоидальный сигнал на входе должен достичь уровня 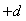 или или 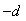 . Непосредственно из функции . Непосредственно из функции 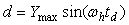 , где , где  - частота колебаний в системе с гистерезисом, можно найти задержку, связанную с гистерезисом: - частота колебаний в системе с гистерезисом, можно найти задержку, связанную с гистерезисом: 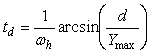 . Понизив с помощью гистерезиса частоту колебаний и измерив ее, можно найти коэффициент передачи объекта на этой частоте по той же формуле (5.20). . Понизив с помощью гистерезиса частоту колебаний и измерив ее, можно найти коэффициент передачи объекта на этой частоте по той же формуле (5.20).
Более подробное рассмотрение процессов в системе с гистерезисом можно найти в работе [Гёльднер].
Недостатком двух последних методов, позволяющих получить точки между 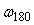 и и 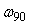 . является невозможность задать заранее требуемую частоту. . является невозможность задать заранее требуемую частоту.
Определение порядка объекта
Методы, описанные выше, дают достаточно информации, чтобы оценить в некоторых случаях порядок объекта управления. Пусть объект описывается передаточной функцией
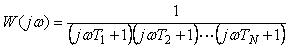 . . |
(5.24)
|
Предположим, что в (5.24) все постоянные времени дают частоты, которые много меньше частоты 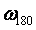 , т.е. , т.е.
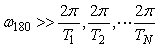 . . |
(5.25)
|
Тогда в окрестности частоты 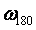 можно пренебречь единицей по сравнению с можно пренебречь единицей по сравнению с 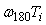 , , 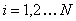 и, беря логарифмы от модуля левой и правой части (5.24), получим: и, беря логарифмы от модуля левой и правой части (5.24), получим: 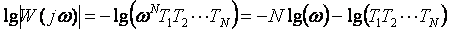 . .
Если с помощью описанных выше методов удалось получить две точки АЧХ (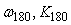 ) и ( ) и (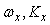 ), то записывая последнее равенство для этих двух точек, получим систему уравнений, из которой можно найти порядок знаменателя передаточной функции объекта управления ), то записывая последнее равенство для этих двух точек, получим систему уравнений, из которой можно найти порядок знаменателя передаточной функции объекта управления 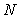 : :
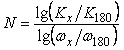 . . |
(5.26)
|
Частота 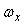 должна быть как можно ближе к должна быть как можно ближе к 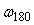 , поскольку наклон нужно искать в окрестности частоты , поскольку наклон нужно искать в окрестности частоты 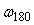 , однако достаточно далеко, чтобы разность частот была много больше погрешности их измерения. , однако достаточно далеко, чтобы разность частот была много больше погрешности их измерения.
Недостатком данного метода является то, что в случае, когда передаточная функция объекта имеет нули, описанный метод дает разность порядков знаменателя и числителя, но не порядок знаменателя.
Заключительные замечания
Описанный выше метод релейной идентификации и его модификации являются в настоящее время самыми распространенными в ПИД регуляторах с автоматической настройкой. Это объясняется следующим достоинствами метода:
- всегда дает результат;
- имеет высокую разрешающую способность;
- не требует сложных вычислений;
- дает результат в рабочей точке.
Метод обладает следующими недостатками:
- не справедлив для большой задержки, когда метод расчета коэффициента передачи дает большую ошибку;
- самостоятельно может использоваться только для очень грубой настройки. В общем случае должен комбинироваться с другими, уточняющими методами идентификации.
5.1.4. Идентификация в замкнутом и разомкнутом контуре
Идентификацию можно выполнять в замкнутом контуре с обратной связью, или в разомкнутом. Идентификация в замкнутом контуре может быть прямой и косвенной. При косвенной идентификации измеряется тестовый сигнал и отклик на него системы с обратной связью, затем путем вычислений по уравнениям системы находится передаточная функция объекта управления. При прямой идентификации передаточная функция объекта находится по измерениям сигналов непосредственно на его входе и выходе.
Если в качестве идентифицирующих воздействий выбирают искусственно созданные возмущения, то такая идентификация называется активной. Если используют сигналы, которые всегда существуют в системе в нормальном режиме ее функционирования, такая идентификация называется пассивной.
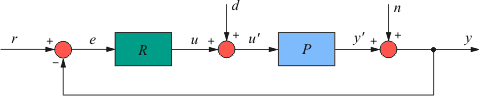
Для дальнейшего изложения нам потребуются уравнения замкнутой системы с ПИД-регулятором. Базовая структура системы показана на рис. 5.27. Здесь 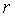 - задающее воздействие (уставка); - задающее воздействие (уставка); 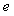 - сигнал ошибки (рассогласование); - сигнал ошибки (рассогласование); 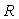 - ПИД-регулятор; - ПИД-регулятор; 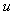 - управляющее воздействие на объект управления - управляющее воздействие на объект управления 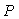 ; ; 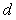 - внешние возмущения; - внешние возмущения;  ; ; 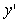 - истинная управляемая величина (может быть измерена только как разность - истинная управляемая величина (может быть измерена только как разность  ); ); 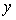 - управляемая величина; - управляемая величина; 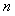 - шум и погрешность измерений. - шум и погрешность измерений.
В системе на рис. 5.27 три входа (три источника сигналов): 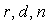 и два выхода (две зависимые переменные и два выхода (две зависимые переменные 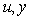 ). Связь между перечисленными величинами можно установить непосредственно по рис. 5.27 в следующем виде: ). Связь между перечисленными величинами можно установить непосредственно по рис. 5.27 в следующем виде:
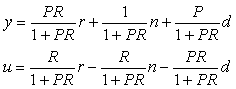 . . |
(5.27)
|
Заметим, что в (5.27) и далее все переменные являются изображениями по Лапласу соответствующих временных функций,  и и  - передаточные функции объекта регулирования и регулятора. Случайные внешние воздействия - передаточные функции объекта регулирования и регулятора. Случайные внешние воздействия 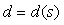 и и 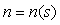 заданы как изображения реализаций случайных процессов. заданы как изображения реализаций случайных процессов.
Идентификация в разомкнутом контуре
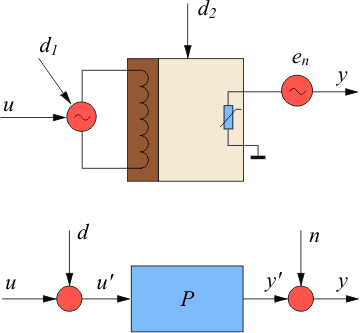
Для идентификации в разомкнутом контуре на объект 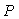 (рис. 5.28) подают входное воздействие (рис. 5.28) подают входное воздействие 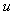 (например, напряжение на нагреватель термошкафа) и измеряют реакцию объекта (например, напряжение на нагреватель термошкафа) и измеряют реакцию объекта 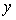 на это воздействие (например, температуру в рабочей зоне). Во время эксперимента на объект воздействуют внешние возмущения на это воздействие (например, температуру в рабочей зоне). Во время эксперимента на объект воздействуют внешние возмущения 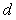 (например, нестабильность напряжения питания (например, нестабильность напряжения питания 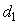 и вариации температуры окружающей среды и вариации температуры окружающей среды 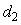 ), а результат измерений суммируется с шумами в канале передачи измерительной информации и с погрешностью средств измерений ), а результат измерений суммируется с шумами в канале передачи измерительной информации и с погрешностью средств измерений 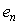 , , 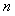 (рис. 5.28). (рис. 5.28).
|
|
|
|
Рис. 5.27. Отображение источников внешних возмущений 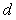 и помех и помех 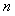 в структуре системы с ПИД-регулятором в структуре системы с ПИД-регулятором
|
Рис. 5.28. Пример объекта управления: термокамера с электрическим нагревом
|
Процесс идентификации состоит в том, что на вход объекта подают тестовые воздействия 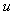 и снимают реакцию объекта и снимают реакцию объекта 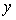 , затем по аналитическим формулам или численными методами оптимизации находят параметры моделей, при которых реакция модели максимально соответствует реакции объекта. , затем по аналитическим формулам или численными методами оптимизации находят параметры моделей, при которых реакция модели максимально соответствует реакции объекта.
Идентификация в разомкнутом контуре является наиболее предпочтительной, поскольку в этом случае отсутствует возможность случайного вывода системы за границы устойчивости. Кроме того, идентификация в разомкнутом контуре позволяет выбрать оптимальные тестовые воздействия, чего нельзя сделать в замкнутом контуре, где спектральная функция входного воздействия на объект управления формируется динамикой контура, независимо от требований экспериментатора. Идентификация в разомкнутом контуре наиболее широко представлена в коммерческих ПИД-регуляторах [Bertocco, O'Dwyer].
Прямая пассивная идентификация в замкнутом контуре
Задача прямой идентификации в замкнутом контуре состоит в нахождении параметров объекта управления 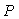 на основании информации, полученной путем измерения реакции системы с обратной связью на основании информации, полученной путем измерения реакции системы с обратной связью 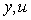 на воздействия на воздействия 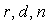 . Пассивная идентификация обладает весьма заманчивым свойством - она не вносит возмущений в нормальный ход технологического процесса, следовательно, совершенно безопасна и не ухудшает качество технологического процесса. . Пассивная идентификация обладает весьма заманчивым свойством - она не вносит возмущений в нормальный ход технологического процесса, следовательно, совершенно безопасна и не ухудшает качество технологического процесса.
Принципиальная возможность пассивной идентификации является предметом споров. В частности, в работе [Ротач] приводятся убедительные аргументы о невозможности пассивной идентификации, однако число патентов на ПИД регуляторы с пассивной идентификацией непрерывно растет нарастающими темпами [Li].
Не вызывает сомнений только то, что достоверность пассивной идентификации существенно ниже, чем активной. Рассмотрим причины этого.
Первая причина состоит в том, что функция спектральной плотности мощности внешних возмущений в реальных объектах быстро спадает с ростом частоты (аналогично шуму 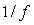 в электронных приборах). Поэтому в наиболее важном участке спектра, включающем частоту в электронных приборах). Поэтому в наиболее важном участке спектра, включающем частоту 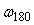 , мощность внешних возмущений оказывается слишком малой, т.е. с точки зрения изложенных в разделе "Выбор тестовых сигналов" требований к тестовым воздействиям внешние возмущения являются наиболее плохим воздействием (см. рис. 5.13), их мощности недостаточно для получения отклика, различимого на фоне шумов в окрестности частоты , мощность внешних возмущений оказывается слишком малой, т.е. с точки зрения изложенных в разделе "Выбор тестовых сигналов" требований к тестовым воздействиям внешние возмущения являются наиболее плохим воздействием (см. рис. 5.13), их мощности недостаточно для получения отклика, различимого на фоне шумов в окрестности частоты 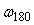 . .
Вторая причина [Изерман, Ротач] касается выбора измеряемых сигналов. Предположим, что 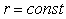 и на систему действует внешнее возмущение и на систему действует внешнее возмущение 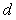 , а , а 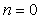 , т.е. измерения выполняются точно. Тогда в силу линейности системы результат идентификации не изменится, если , т.е. измерения выполняются точно. Тогда в силу линейности системы результат идентификации не изменится, если  . Подставив в (5.27) . Подставив в (5.27) 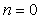 и и  , получим: , получим:
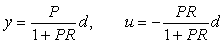 . Поскольку целью идентификации является нахождение передаточной функции объекта 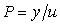 , то, подставив сюда полученные выше значения , то, подставив сюда полученные выше значения 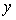 и и 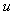 , получим: , получим:
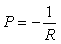 . Таким образом, передаточную функцию объекта невозможно получить, измеряя 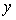 и и 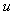 при внешних воздействиях при внешних воздействиях  . Причина состоит в том, что мы не можем измерить воздействие на объект . Причина состоит в том, что мы не можем измерить воздействие на объект 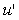 , а измеряемая в эксперименте величина , а измеряемая в эксперименте величина 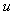 получается после прохождения сигнала получается после прохождения сигнала 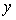 через регулятор через регулятор 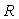 . Поэтому описанным экспериментом можно идентифицировать только регулятор, но не объект. . Поэтому описанным экспериментом можно идентифицировать только регулятор, но не объект.
Однако пассивная идентификация становится возможной, если в качестве тестового сигнала использовать сигнал уставки 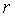 в период его изменения по алгоритму функционирования системы управления. Например, для электрического паяльника такой сигнал появляется в момент изменения уставки температуры жала паяльника. В конвекционной печи для монтажа радиоэлементов такой сигнал появляется при алгоритмическом переключении температурного режима печи. В обоих случаях для идентификации используются уже имеющиеся в системе сигналы, при этом нормальный ход технологического процесса не нарушается. Поэтому такая идентификация является пассивной. в период его изменения по алгоритму функционирования системы управления. Например, для электрического паяльника такой сигнал появляется в момент изменения уставки температуры жала паяльника. В конвекционной печи для монтажа радиоэлементов такой сигнал появляется при алгоритмическом переключении температурного режима печи. В обоих случаях для идентификации используются уже имеющиеся в системе сигналы, при этом нормальный ход технологического процесса не нарушается. Поэтому такая идентификация является пассивной.
Итак, выберем 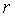 в качестве тестового (идентифицирующего) воздействия. Тогда, предполагая, что измерения выполняются точно ( в качестве тестового (идентифицирующего) воздействия. Тогда, предполагая, что измерения выполняются точно (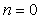 ), а уровень тестового воздействия высок по сравнению с внешними возмущениями ( ), а уровень тестового воздействия высок по сравнению с внешними возмущениями (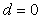 ), из (5.27) получим ), из (5.27) получим
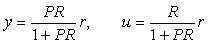 , или , или 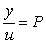 , , |
(5.28)
|
т.е. прямая пассивная идентификация объекта по сигналам на его входе и выходе позволяет найти передаточную функцию объекта, если в качестве тестового воздействия используется изменение сигнала уставки 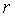 . .
Косвенная идентификация в замкнутом контуре
Для косвенной идентификации тестовое воздействие подают на вход системы 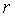 и измеряют реакцию на него и измеряют реакцию на него 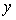 . Передаточную функцию объекта . Передаточную функцию объекта 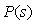 можно найти из первого уравнения в (5.27): можно найти из первого уравнения в (5.27):
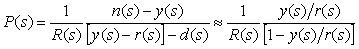 . . |
(5.29)
|
Шумы измерений 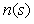 и внешние возмущения и внешние возмущения 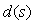 в уравнении (5.29) часто полагают равными нулю, или учитывают как погрешность идентификации. Полученная передаточная функция в уравнении (5.29) часто полагают равными нулю, или учитывают как погрешность идентификации. Полученная передаточная функция 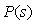 используется далее для идентификации параметров выбранной модели (см. раздел "Модели объектов управления"). используется далее для идентификации параметров выбранной модели (см. раздел "Модели объектов управления").
Как видим, для косвенной идентификации необходимо знать передаточную функцию регулятора 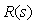 . Поэтому косвенная идентификация не осуществима на этапе, когда регулятор еще не синтезирован. . Поэтому косвенная идентификация не осуществима на этапе, когда регулятор еще не синтезирован.
Косвенная идентификация обычно мало эффективна [Изерман] и она требует выполнения условий идентифицируемости в замкнутом контуре, которые выполняются не всегда [Штейнберг, Изерман, Справочник].
Прямая активная идентификация в замкнутом контуре
Прямая активная идентификация выполняется точно так, как прямая пассивная с сигналом 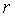 (см. выше и (5.28)), однако сигнал (см. выше и (5.28)), однако сигнал 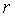 задается искусственно. Его величина и длительность выбираются из значений, допустимых для нормального хода технологического процесса. задается искусственно. Его величина и длительность выбираются из значений, допустимых для нормального хода технологического процесса.
5.1.5. Аналитическая идентификация
После того, как найдена передаточная функция объекта управления или его импульсная (или переходная) характеристика, возникает задача определения параметров модели объекта управления. Существует два подхода к решению этой задачи: аналитический (по формулам) и с помощью численных методов оптимизации. Преимуществом аналитической идентификации является низкая вычислительная сложность, что позволяет использовать ее в ПИД-регуляторах с маломощными контроллерами, но она позволяет идентифицировать параметры только очень простых моделей. Идентификация численными методами используется в универсальных программных пакетах, которые продаются независимо от ПИД-регуляторов и применяются для их настройки с помощью персональных компьютеров.
Идентификация модели первого порядка по средней длительности переходного процесса
В случае, когда переходный процесс описывается моделью первого порядка с задержкой (5.1), его длительность нельзя характеризовать одним параметром "постоянная времени", как для процессов без задержки. Поэтому используется понятие "средняя длительность переходного процесса" (average residence time [Astrom]) которое определяется как
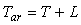 , , |
(5.30)
|
где  - постоянная времени, - постоянная времени, 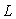 - транспортная задержка (см. также (5.3)). - транспортная задержка (см. также (5.3)).
Используя понятие средней длительности переходного процесса, можно сформулировать один из вариантов критерия, при котором кривые объекта и модели первого порядка (5.3) можно считать приблизительно совпадающими. Это условие состоит в пересечении переходных характеристик модели и объекта на уровне 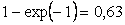 (рис. 5.29). Поскольку в точке пересечения в уравнении (5.3) (рис. 5.29). Поскольку в точке пересечения в уравнении (5.3) 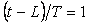 , отсюда можно получить, что абсцисса точки пересечения , отсюда можно получить, что абсцисса точки пересечения 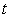 равна равна 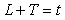 , см. рис. 5.29. В этом уравнении два неизвестных: , см. рис. 5.29. В этом уравнении два неизвестных:  и и  . .
Для определения  проводят касательную в точке максимального угла наклона касательной (на рис. 5.29 это касательная в точке "Максимальный угол наклона"). При этом задержка проводят касательную в точке максимального угла наклона касательной (на рис. 5.29 это касательная в точке "Максимальный угол наклона"). При этом задержка  должна определяться в точке пересечения касательной с осью времени. должна определяться в точке пересечения касательной с осью времени.
|
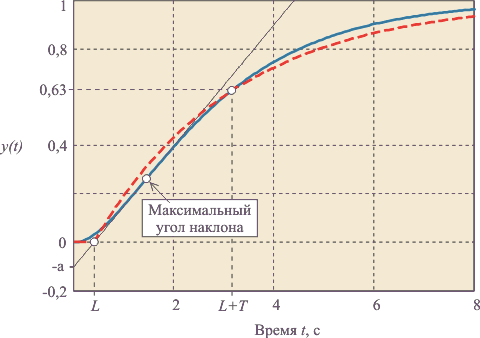
|
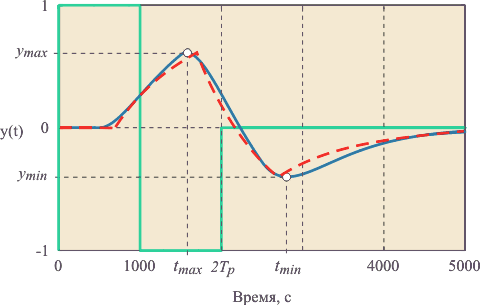
|
|
Рис. 5.29. Переходная характеристика объекта второго порядка (сплошная линия) и его аппроксимация моделью (5.3) (штриховая линия)
|
Рис. 5.30. Реакция системы второго порядка (синяя линия) на двойной прямоугольный импульс (зеленая линия) и ее аппроксимация моделью первого порядка (красная штриховая линия)
|
Коэффициент 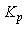 модели первого порядка (5.3) определяется как отношение установившегося значения выходной переменной к амплитуде тестового скачка. Предварительно из выходной переменной вычитается ее значение при модели первого порядка (5.3) определяется как отношение установившегося значения выходной переменной к амплитуде тестового скачка. Предварительно из выходной переменной вычитается ее значение при 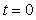 . .
График переходного процесса идентифицированной описанным способом модели (5.3) при 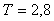 и и 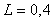 показан штриховой линией на рис. 5.29. показан штриховой линией на рис. 5.29.
Поскольку из рис. 5.29 следует, что тангенс наклона касательной равен 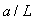 , для интегрирующего процесса (5.12), (5.13) получим , для интегрирующего процесса (5.12), (5.13) получим 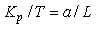 . .
Метод двойного прямоугольного импульса
Метод аналитической идентификации по характерным точкам реакции объекта на двойной прямоугольный импульс хорош тем, что после окончания тестового воздействия система переходит в исходное состояние, а также тем, что этот метод требует мало времени, поскольку после прохождения откликом минимума (рис. 5.30) эксперимент можно считать законченным. На кривой отклика системы на двойной прямоугольный импульс находят точку максимума и минимума. Зная координаты этих точек (см. рис. 5.30), можно найти все параметры модели первого порядка с задержкой по следующим формулам [Astrom]:
Смысл использованных здесь обозначений понятен из рис. 5.30; 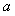 - амплитуда тестового импульса (на рис. 5.30 параметр - амплитуда тестового импульса (на рис. 5.30 параметр 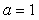 ). Величина транспортной задержки ). Величина транспортной задержки 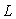 имеет два значения, рассчитанные по двум формулам. Близость полученных значений может служить признаком качества аппроксимации. имеет два значения, рассчитанные по двум формулам. Близость полученных значений может служить признаком качества аппроксимации.
Для вывода этих формул [Astrom] нужно по рис. 5.30 записать выражения для точек максимума и минимума, зная, что реакция системы 1-го порядка на скачок имеет вид (5.1) и учитывая, что для системы первого порядка 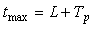 : :
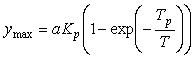 , 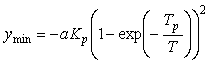 , 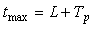 , 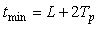 . Далее, решая полученную систему уравнений относительно неизвестных 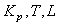 , получим (5.31). Для нахождения , получим (5.31). Для нахождения 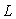 получаем два варианта выражений. получаем два варианта выражений.
Недостатком метода является невозможность точного определения коэффициента передачи объекта в статике 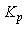 , поскольку эксперимент заканчивается до наступления установившегося режима. Кроме того, проблематично определить время , поскольку эксперимент заканчивается до наступления установившегося режима. Кроме того, проблематично определить время 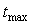 и и 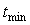 с большой точностью. с большой точностью.
Использование результатов частотной идентификации
Величины 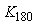 и и 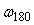 , полученные в результате эксперимента с релейным регулятором (см. "Частотная идентификация в режиме релейного регулирования"), можно использовать для аналитического определения параметров , полученные в результате эксперимента с релейным регулятором (см. "Частотная идентификация в режиме релейного регулирования"), можно использовать для аналитического определения параметров  и и 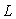 модели первого порядка. Для этого запишем выражение для квадрата модуля коэффициента передачи модели (5.5) на частоте модели первого порядка. Для этого запишем выражение для квадрата модуля коэффициента передачи модели (5.5) на частоте 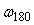 : :
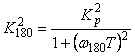 . Если параметр 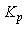 известен, например, из результатов анализа реакции объекта на скачок (5.3), то, решая предыдущее уравнение относительно искомого известен, например, из результатов анализа реакции объекта на скачок (5.3), то, решая предыдущее уравнение относительно искомого  , получим: , получим:
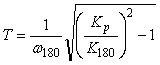 . . |
(5.32)
|
Транспортную задержку 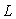 можно найти из уравнения для суммарного сдвига фаз на частоте можно найти из уравнения для суммарного сдвига фаз на частоте 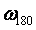 : :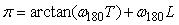 , откуда , откуда
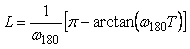 . . |
(5.33)
|
К сожалению, все формулы из этого раздела получены только для модели 1-го порядка. Аналогичные выражения для моделей более высокого порядка аналитически получить не удается или они оказываются чрезмерно громоздкими. Поэтому для идентификации параметров моделей более высоких порядков используют численные методы оптимизации (минимизации).
5.1.6. Методы минимизации критериальной функции
Описанные методы расчета параметров моделей по формулам удобны тем, что идентификация выполняется очень просто и может быть реализована в маломощном микропроцессоре. Однако их существенными недостатками являются:
- невозможность (или чрезмерная сложность) идентификации параметров моделей выше 1‑го порядка;
- большая погрешность метода;
- отсутствие фильтрации шумов в процессе идентификации.
Более качественные результаты могут быть получены при использовании численных методов оптимизации. Для их выполнения составляется критериальная функция 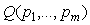 с параметрами с параметрами  , которая характеризует степень близости между откликом модели и откликом объекта на одно и то же входное воздействие. Обычно критериальная функция выбирается в виде суммы квадратов отклонений искомой функции , которая характеризует степень близости между откликом модели и откликом объекта на одно и то же входное воздействие. Обычно критериальная функция выбирается в виде суммы квадратов отклонений искомой функции 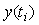 от экспериментальных данных от экспериментальных данных 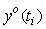 : :
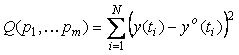 , , |
(5.34)
|
|
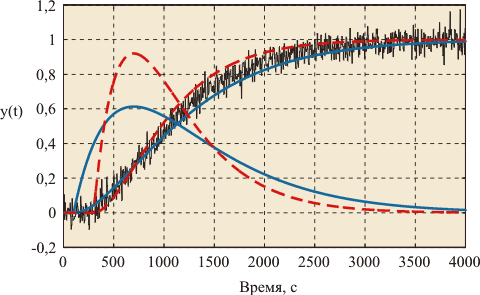
|
|
Рис. 5.31. Два варианта переходных характеристик с примерно одинаковой среднеквадратической погрешностью и импульсные характеристики, полученные их дифференцированием
|
где 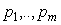 - параметры, которые требуется найти; - параметры, которые требуется найти; 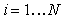 - номер временного такта, при котором измеряется значение функции. Такой выбор критериальной функции не является единственным. Может быть использован, например, модуль максимального отклонения, модуль от арифметического среднего, и др. Различные критерии дадут слегка отличающиеся значения параметров модели. Однако среднеквадратичный критерий (5.34) имеет замечательное свойство: он дает максимально правдоподобную оценку искомых параметров. Иначе говоря, если ввести понятие вероятности того, что полученная кривая проходит так, как истинные данные в отсутствие шума, то при использовании среднеквадратического критерия эта вероятность будет максимальной. Это справедливо, если данные, полученные при измерениях, являются статистически независимыми величинами (т.е. если интервал между отсчетами выбран больше, чем время корреляции шума), если отсутствует систематическая погрешность измерений, если измерения распределены по нормальному закону (Гаусса) и параметры этого распределения одинаковы для всех точек на кривой - номер временного такта, при котором измеряется значение функции. Такой выбор критериальной функции не является единственным. Может быть использован, например, модуль максимального отклонения, модуль от арифметического среднего, и др. Различные критерии дадут слегка отличающиеся значения параметров модели. Однако среднеквадратичный критерий (5.34) имеет замечательное свойство: он дает максимально правдоподобную оценку искомых параметров. Иначе говоря, если ввести понятие вероятности того, что полученная кривая проходит так, как истинные данные в отсутствие шума, то при использовании среднеквадратического критерия эта вероятность будет максимальной. Это справедливо, если данные, полученные при измерениях, являются статистически независимыми величинами (т.е. если интервал между отсчетами выбран больше, чем время корреляции шума), если отсутствует систематическая погрешность измерений, если измерения распределены по нормальному закону (Гаусса) и параметры этого распределения одинаковы для всех точек на кривой  . В этом случае задача минимизации (5.34) совпадает с задачей оптимальной фильтрации сигнала . В этом случае задача минимизации (5.34) совпадает с задачей оптимальной фильтрации сигнала 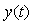 на фоне шума [Косарев] (см. также рис. 5.1, рис. 5.2). Иначе говоря, процесс минимизации критерия (5.34) является одновременно процессом оптимальной фильтрации, поэтому применение дополнительных фильтров нижних частот приводит не к уменьшению, а к увеличению погрешности идентификации. на фоне шума [Косарев] (см. также рис. 5.1, рис. 5.2). Иначе говоря, процесс минимизации критерия (5.34) является одновременно процессом оптимальной фильтрации, поэтому применение дополнительных фильтров нижних частот приводит не к уменьшению, а к увеличению погрешности идентификации.
В случае, когда шум имеет не нормальное распределение, квадратичный критерий (5.34) не дает максимально правдоподобную оценку параметров искомой функции. Например, для распределения Лапласа оптимальной критериальной функцией будет сумма модулей отклонений [Цыпкин]. Однако в подавляющем большинстве практически важных случаев шум оказывается распределенным по нормальному закону.
Результаты измерений отклика объекта на тестовые воздействия содержат как высокочастотные шумы, так и низкочастотные возмущения, лежащих в той же области спектра, что и полезный сигнал. Высокочастотные шумы легко убрать с помощью цифрового фильтра или в процессе минимизации критериальной функции (5.34). Однако, если время автокорреляции внешних возмущений сравнимо с длительностью измерений, то для каждого нового эксперимента мы будем получать различные параметры модели объекта. К сожалению, данная проблема не может быть решена статистическими методами при жестких требованиях к быстроте идентификации в ПИД-регуляторах. Только увеличение амплитуды тестового воздействия, компенсация внешних возмущений и корректировка результатов эксперимента в соответствии с условиями его проведения могут увеличить достоверность полученных данных.
Для того, чтобы учесть различную ценность информации на разных участках переходного процесса, в выражения для критериальной функции вводят весовую функцию 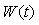 : :
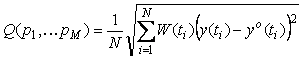 . . |
(5.35)
|
|
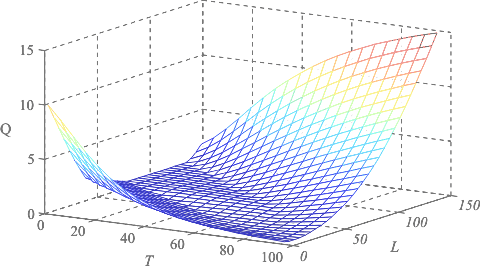
|
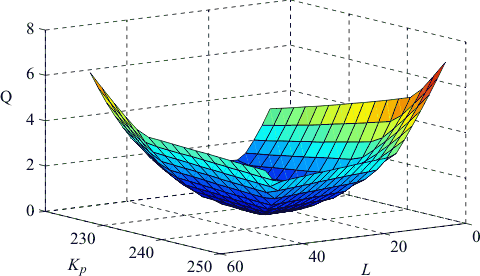
|
|
Рис. 5.32. Сечение критериальной функции в точке минимума в зависимости от 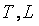 для критерия (5.35) при идентификации модели термошкафа (см. рис. 5.3) в форме (5.8) для критерия (5.35) при идентификации модели термошкафа (см. рис. 5.3) в форме (5.8)
|
Рис. 5.33. Сечение критериальной функции в точке минимума в зависимости от 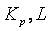 для критерия (5.35) при идентификации модели термошкафа (см. рис. 5.3) в форме (5.8) для критерия (5.35) при идентификации модели термошкафа (см. рис. 5.3) в форме (5.8)
|
Для выбора вида 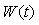 нужно заранее знать вид функции отклика нужно заранее знать вид функции отклика 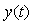 . В диалоговом режиме идентификации, когда пользователь может наблюдать на экране компьютера различие между . В диалоговом режиме идентификации, когда пользователь может наблюдать на экране компьютера различие между 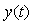 и и 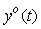 , вид функции , вид функции 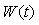 можно подобрать интуитивно. Однако в ПИД регуляторах с автонастройкой этот процесс невозможен, поэтому в алгоритм идентификации должны быть заложены эвристические правила выбора весовой функции. Поскольку конечной целью идентификации является не минимизация погрешности аппроксимации, а получение заданного качества регулирования при ограничении на робастность, то вид критериальной функции может быть уточнен после синтеза регулятора и получения оценок его характеристик. можно подобрать интуитивно. Однако в ПИД регуляторах с автонастройкой этот процесс невозможен, поэтому в алгоритм идентификации должны быть заложены эвристические правила выбора весовой функции. Поскольку конечной целью идентификации является не минимизация погрешности аппроксимации, а получение заданного качества регулирования при ограничении на робастность, то вид критериальной функции может быть уточнен после синтеза регулятора и получения оценок его характеристик.
Отметим, что близость функций не гарантирует близости их производных 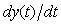 и и 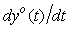 . На рис. 5.31 показаны два варианта переходных характеристик. Оба варианта достаточно близко соответствуют переходной характеристике объекта (зашумленная кривая), однако их производные (импульсные характеристики) отличаются очень сильно (две кривые колоколообразной формы), хотя именно точка максимума импульсной характеристики указывает величину средней длительности переходного процесса, которая используется в расчете параметров ПИД-регулятора. Поэтому в критериальную функцию при идентификации параметров моделей желательно добавлять и критерий близости производных. . На рис. 5.31 показаны два варианта переходных характеристик. Оба варианта достаточно близко соответствуют переходной характеристике объекта (зашумленная кривая), однако их производные (импульсные характеристики) отличаются очень сильно (две кривые колоколообразной формы), хотя именно точка максимума импульсной характеристики указывает величину средней длительности переходного процесса, которая используется в расчете параметров ПИД-регулятора. Поэтому в критериальную функцию при идентификации параметров моделей желательно добавлять и критерий близости производных.
С помощью критериальной функции задача параметрической идентификации сводится к задаче нахождения параметров модели 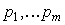 , при которых критериальная функция достигает минимума. Примеры сечений критериальной функции вида (5.35) для модели (5.8) при идентификации термошкафа (рис. 5.1) приведены на рис. 5.32, рис. 5.33. , при которых критериальная функция достигает минимума. Примеры сечений критериальной функции вида (5.35) для модели (5.8) при идентификации термошкафа (рис. 5.1) приведены на рис. 5.32, рис. 5.33.
При решении задачи минимизации критериальной функции возникает ряд численных проблем, часто связанных с плохой обусловленностью системы линейных уравнений, наличием нескольких минимумов и овражным характером критериальной функции (рис. 5.32). Поэтому традиционный метод наименьших квадратов (МНК) часто не позволяет получить решение задачи при попытке найти параметры моделей высокого порядка при малом количестве информации в исходных данных. Решению этих проблем посвящено множество книг и статей. Хорошие результаты дает метод сингулярной декомпозиции матриц (SVD) [Numerical] в сочетании с многошаговыми методами интегрирования дифференциальных уравнений [Ljung, Ljung], а также разновидности метода Монте-Карло. При поиске глобального минимума хорошие результаты дают генетические алгоритмы [Гладков].
|
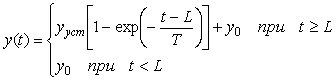 ,
,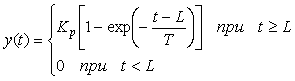 ,
,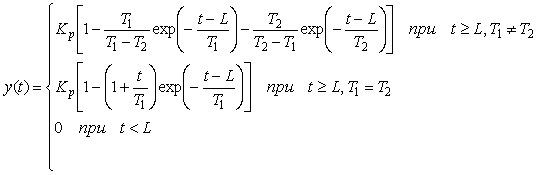 .
.



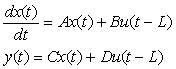 при
при 

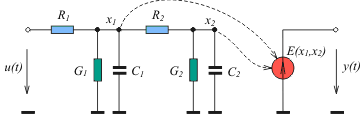

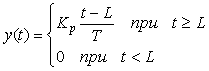 ,
,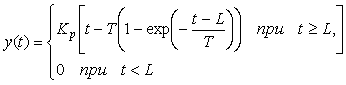
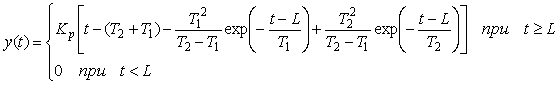


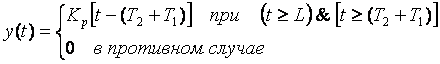 , а переходная функция - в
, а переходная функция - в 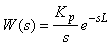 .
.












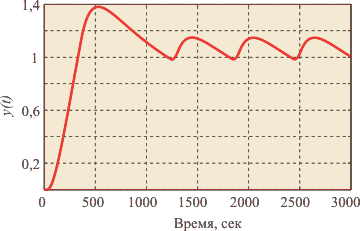
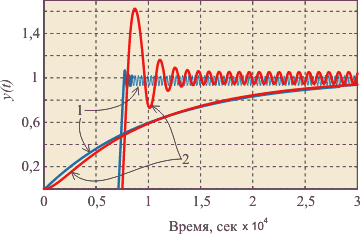


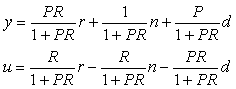 .
.



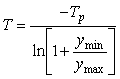 ,
, 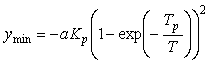 ,
,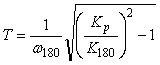 .
.









