5.3. Модификации ПИД-регуляторов
Постоянно растущие требования рынка к снижению времени регулирования, к качеству переходного процесса, к степени ослаблению влияния внешних возмущений и шумов, к упрощению процедуры настройки и необходимость управления объектами с большой транспортной задержкой инициировали появление множества модификаций ПИД-регуляторов.
5.3.1. Регулятор с весовыми коэффициентами при уставке
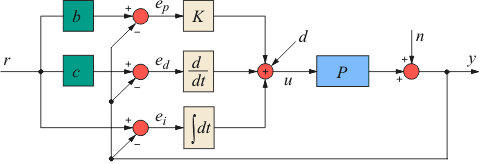
В классическом ПИД-регуляторе сигнал ошибки 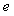 равен разности между задающим воздействием равен разности между задающим воздействием 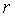 и выходной переменной объекта и выходной переменной объекта 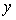 : : 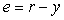 . Однако качество регулирования можно улучшить, если ошибку вычислять отдельно для пропорциональной, дифференциальной и интегральной составляющей [Astrom] (рис. 5.43): . Однако качество регулирования можно улучшить, если ошибку вычислять отдельно для пропорциональной, дифференциальной и интегральной составляющей [Astrom] (рис. 5.43):
где 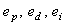 - ошибка для пропорциональной, дифференциальной и интегральной составляющей; - ошибка для пропорциональной, дифференциальной и интегральной составляющей; 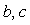 - настроечные весовые коэффициенты. - настроечные весовые коэффициенты.
|
|
|
Рис. 5.43. ПИД-регулятор с весовыми коэффициентами b и c при уставке
|
Уравнение такого регулятора аналогично (5.36):
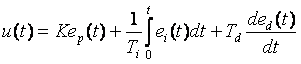 |
(5.54)
|
Отметим, что весовой коэффициент при интегральной составляющей отсутствует, что необходимо для обеспечения нулевой ошибки в установившемся режиме.
Пользуясь выражениями (5.53), (5.54), а также рис. 5.43 и переходя к изображениям по Лапласу, уравнение регулятора можно записать в виде
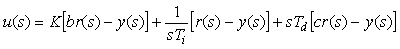 = =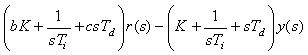 |
(5.55)
|
Можно заметить, что второе слагаемое здесь содержит передаточную функцию классического ПИД-регулятора (5.39). Поэтому регулятор, представленный на рис. 5.43, можно заменить эквивалентным ему регулятором, показанным на рис. 5.44, если блок 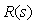 останется классическим регулятором (5.40), а блок останется классическим регулятором (5.40), а блок 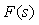 будет иметь передаточную функцию вида будет иметь передаточную функцию вида
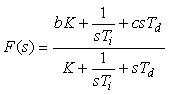 . . |
(5.56)
|
 |
|
Рис. 5.44. Выделение блока 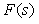 в структуре ПИД-регулятора в структуре ПИД-регулятора
|
Структура полученного регулятора имеет замечательное свойство: блок 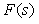 не входит в контур регулирования. Это означает, что робастность, качество регулирования, реакция на шумы и внешние возмущения по-прежнему будут определяться только параметрами не входит в контур регулирования. Это означает, что робастность, качество регулирования, реакция на шумы и внешние возмущения по-прежнему будут определяться только параметрами 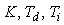 , т.е. параметры блоков , т.е. параметры блоков 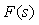 ( (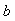 и и 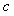 ) настраиваются независимо от параметров ) настраиваются независимо от параметров 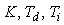 . .
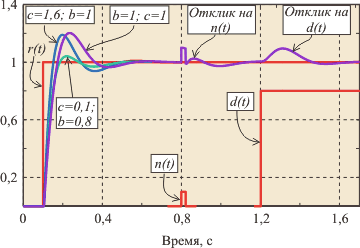
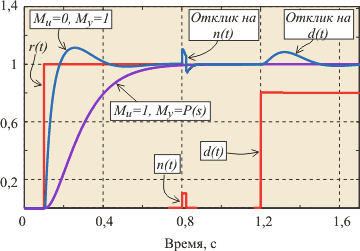
Параметры 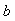 и и 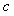 определяют вид АЧХ блока определяют вид АЧХ блока 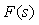 и позволяют улучшить качество реакции регулятора на изменение уставки и позволяют улучшить качество реакции регулятора на изменение уставки 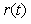 . На рис. 5.45 показана реакция замкнутой системы с описанным регулятором при разных значениях весовых коэффициентов . На рис. 5.45 показана реакция замкнутой системы с описанным регулятором при разных значениях весовых коэффициентов 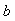 и и 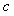 . Как видно из рисунка, изменение параметров . Как видно из рисунка, изменение параметров 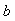 и и 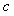 не влияет на отклик системы на шумы не влияет на отклик системы на шумы 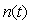 и внешние возмущения и внешние возмущения 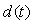 . .
Коэффициент 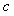 часто выбирают равным нулю, чтобы избежать дифференцирования случайных резких выбросов в управляющем сигнале часто выбирают равным нулю, чтобы избежать дифференцирования случайных резких выбросов в управляющем сигнале 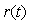 , если они возможны. , если они возможны.
Описанный регулятор при 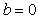 и и 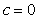 иногда называют И-ПД регулятором, а при иногда называют И-ПД регулятором, а при 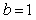 и и 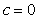 - ПИ-Д регулятором. - ПИ-Д регулятором.
5.3.2. Регулятор с формирующим фильтром для сигнала уставки
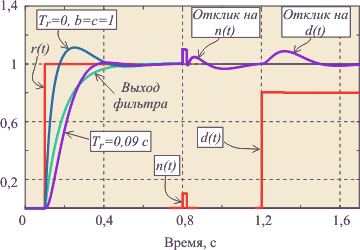
Дальнейшим усовершенствованием регулятора со структурой, показанной на рис. 5.44, является применение фильтра в блоке 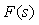 , передаточная функция которого приобретает вид , передаточная функция которого приобретает вид
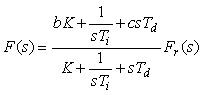 , , |
(5.57)
|
где 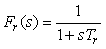 . . |
(5.58)
|
Здесь 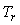 - постоянная времени фильтра, которую можно найти следующим образом. Предположим, что модуль передаточной функции (5.57) при - постоянная времени фильтра, которую можно найти следующим образом. Предположим, что модуль передаточной функции (5.57) при 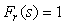 имеет выброс (аналогичный выбросу на рис. 5.41). Величина такого выброса на АЧХ замкнутой системы характеризуется параметром "колебательность" имеет выброс (аналогичный выбросу на рис. 5.41). Величина такого выброса на АЧХ замкнутой системы характеризуется параметром "колебательность" 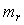 , который равен отношению коэффициента передачи в точке максимума (обозначим ее , который равен отношению коэффициента передачи в точке максимума (обозначим ее 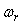 ) к коэффициенту передачи на нулевой частоте. Этот максимум можно убрать, если потребовать, чтобы на частоте ) к коэффициенту передачи на нулевой частоте. Этот максимум можно убрать, если потребовать, чтобы на частоте 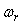 модуль коэффициента передачи фильтра был равен модуль коэффициента передачи фильтра был равен 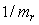 . Из этого условия можно получить значение постоянной времени фильтра . Из этого условия можно получить значение постоянной времени фильтра 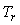 : :
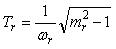 . . |
(5.59)
|
Пример реакции системы с регулятором, использующим формирующий фильтр, приведен на рис. 5.46.
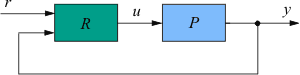
5.3.3. Принцип разомкнутого управления
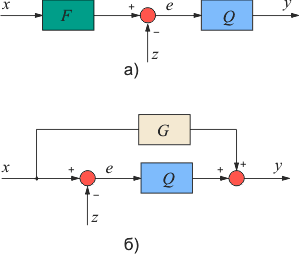
Регулятор можно построить и без использования обратной связи. Если известны действующие на систему возмущения и желаемая реакция на изменение управляющего воздействия, то в некоторых случаях можно найти такую передаточную функцию регулятора, при которой получается желаемая реакция системы. Достоинством такого подхода является высокая скорость реагирования системы на внешние возмущения, поскольку для выработки управляющего воздействия не нужно ждать, пока управляющий сигнал пройдет через объект и возвратится в регулятор по цепи обратной связи. Кроме того, система с разомкнутым управлением в принципе не может быть неустойчивой, поскольку в ней отсутствует обратная связь.
Недостатком является принципиальная невозможность получения высокой точности при неизвестных возмущениях и низкой точности модели объекта, невозможность полной компенсации возмущений для объектов с транспортной задержкой и проблема физической реализуемости обратных операторов.
В зарубежной литературе системы с разомкнутым управлением называют системами с "прямой связью". Термин "прямая связь" выбран для того, чтобы подчеркнуть отличие этого метода от метода обратной связи. Ниже оба термина будут использованы как синонимы.
Достоинства разомкнутого и замкнутого управления можно объединить в одном регуляторе. Наилучшие характеристики системы получаются, если ее проектировать по принципу разомкнутого управления, а обратную связь использовать только для дальнейшей минимизации погрешности.
В предыдущем параграфе был рассмотрен частный случай прямой связи, которая реализована с помощью блока 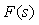 (рис. 5.44). Основной принцип применения разомкнутого управления в ПИД-регуляторах состоит в следующем. Задача проектирования делится на две части. Первая часть - обеспечение робастности и ослабления влияния шумов и внешних возмущений - решается с помощью параметров (рис. 5.44). Основной принцип применения разомкнутого управления в ПИД-регуляторах состоит в следующем. Задача проектирования делится на две части. Первая часть - обеспечение робастности и ослабления влияния шумов и внешних возмущений - решается с помощью параметров 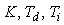 . Вторая часть - обеспечение заданной реакции на управляющее воздействие . Вторая часть - обеспечение заданной реакции на управляющее воздействие 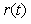 - решается с помощью параметров регулятора с прямой связью. Регуляторы, обеспечивающие возможность независимого решения этих двух задач называют "регуляторами с двумя степенями свободы" и на их условном изображении присутствуют два входа (рис. 5.48). - решается с помощью параметров регулятора с прямой связью. Регуляторы, обеспечивающие возможность независимого решения этих двух задач называют "регуляторами с двумя степенями свободы" и на их условном изображении присутствуют два входа (рис. 5.48).
Структура ПИД-регулятора, использующего принцип разомкнутого управления, показана на рис. 5.47. Здесь регулятор 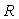 спроектирован как в системе с классическим ПИД-регулятором, а передаточные функции блоков спроектирован как в системе с классическим ПИД-регулятором, а передаточные функции блоков  и и 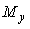 выбираются так, чтобы улучшить реакцию системы на входное воздействие выбираются так, чтобы улучшить реакцию системы на входное воздействие 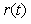 . .
|
|
|
|
Рис. 5.47. Регулятор, комбинирующий принцип разомкнутого управления и принцип обратной связи
|
Рис. 5.48. Регулятор с двумя степенями свободы - обобщение классического ПИД-регулятора
|
Принцип действия системы состоит в следующем. Изменение сигнала 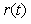 поступает на вход объекта управления поступает на вход объекта управления 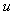 через блок через блок  , минуя цепь обратной связи. Передаточная функция блока , минуя цепь обратной связи. Передаточная функция блока  выбирается таким образом, чтобы выходной сигнал системы выбирается таким образом, чтобы выходной сигнал системы 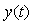 в точности соответствовал входному сигналу, в точности соответствовал входному сигналу, 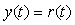 , т.е. чтобы сигнал ошибки , т.е. чтобы сигнал ошибки 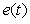 был равен нулю. Поскольку в реальной системе при воздействии внешних возмущений или изменении уставки был равен нулю. Поскольку в реальной системе при воздействии внешних возмущений или изменении уставки 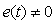 , то вступает в действие обычный ПИД-регулятор , то вступает в действие обычный ПИД-регулятор 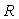 , который с помощью обратной связи пытается свести появившуюся ошибку к нулю. , который с помощью обратной связи пытается свести появившуюся ошибку к нулю.
Непосредственно по рис. 5.47 можно записать передаточную функцию системы от входа 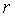 к ее выходу к ее выходу 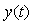 (для начала положим (для начала положим 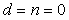 ): ):
Отсюда передаточную функцию замкнутой системы можно записать в виде
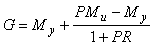 . . |
(5.61)
|
Здесь первый член выбирают, как следует из описанного выше принципа действия системы, так, чтобы в идеальных условиях 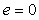 и и 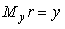 , т.е. желаемой передаточной функцией системы является , т.е. желаемой передаточной функцией системы является 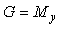 . Поэтому второй член в (5.61) необходимо сделать равным нулю. Этого можно достичь двумя способами. Первый из них состоит в том, чтобы сделать бесконечно большим петлевое усиление . Поэтому второй член в (5.61) необходимо сделать равным нулю. Этого можно достичь двумя способами. Первый из них состоит в том, чтобы сделать бесконечно большим петлевое усиление 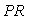 . Чаще используют второй путь, который состоит в выборе такой передаточной функции . Чаще используют второй путь, который состоит в выборе такой передаточной функции  , чтобы выполнялось соотношение , чтобы выполнялось соотношение 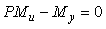 , т.е. , т.е.
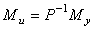 . . |
(5.62)
|
Таким образом, в отличие от регулятора с обратной связью, у которого точность обеспечивается благодаря делению сигнала ошибки на большое число (усиление интегратора), в регуляторах с прямой связью точность обеспечивается путем компенсации ошибки, т.е. с помощью операции вычитания.
Поскольку в системе, показанной на рис. 5.47, ошибка на низких частотах и в установившемся режиме равна нулю благодаря интегральному члену в ПИД-регуляторе 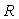 , высокую точность компенсации ошибки с помощью прямой связи достаточно обеспечить только на высоких частотах. Это облегчает задачу синтеза передаточной функции , высокую точность компенсации ошибки с помощью прямой связи достаточно обеспечить только на высоких частотах. Это облегчает задачу синтеза передаточной функции  . .
Нахождение обратной динамики объекта
Как следует из (5.62), для нахождения передаточной функции  необходимо найти обратный оператор необходимо найти обратный оператор 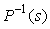 . Благодаря алгебраической форме изображений операторов по Лапласу, формально сделать это достаточно просто. Например, для объекта с передаточной функцией (5.5) обратный оператор будет равен . Благодаря алгебраической форме изображений операторов по Лапласу, формально сделать это достаточно просто. Например, для объекта с передаточной функцией (5.5) обратный оператор будет равен
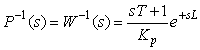 . . |
(5.63)
|
Однако такие операции наталкиваются на проблему физической реализуемости. Выражение (5.63) содержит член 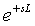 , который является обратным по отношению к идеальной задержке, т.е. является изображением операции идеального предсказания. Кроме того, для реализации (5.63) необходима операция идеального дифференцирования, реализация которой также достаточно проблематична. , который является обратным по отношению к идеальной задержке, т.е. является изображением операции идеального предсказания. Кроме того, для реализации (5.63) необходима операция идеального дифференцирования, реализация которой также достаточно проблематична.
Рассмотрим другой пример. Пусть передаточная функция объекта описывается выражением 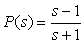 . Обратный оператор имеет вид . Обратный оператор имеет вид 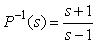 . Однако полюс передаточной функции . Однако полюс передаточной функции 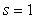 лежит в правой полуплоскости, что свидетельствует о неустойчивости системы, описываемой обратным оператором. лежит в правой полуплоскости, что свидетельствует о неустойчивости системы, описываемой обратным оператором.
Следующей проблемой является компенсация полюсов передаточной функции  нулями, появившимися после обращения оператора нулями, появившимися после обращения оператора 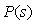 в (5.62). Как будет показано ниже, такая компенсация может привести к резкому различию времени реакции системы на изменение уставки и на внешние возмущения. в (5.62). Как будет показано ниже, такая компенсация может привести к резкому различию времени реакции системы на изменение уставки и на внешние возмущения.
Для решения перечисленных проблем нужно наложить ограничения на вид передаточной функции 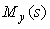 . При этом соотношения . При этом соотношения 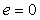 и и 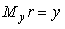 уже не будут выполняться точно, однако появляется возможность физической реализации обратного оператора уже не будут выполняться точно, однако появляется возможность физической реализации обратного оператора 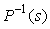 . .
Во-первых, необходимо потребовать, чтобы транспортная задержка блока 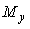 была не менее транспортной задержки объекта была не менее транспортной задержки объекта 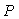 . Это исключает необходимость предсказания. . Это исключает необходимость предсказания.
Во-вторых, если 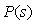 имеет полюса в правой полуплоскости, то они должны совпадать с полюсами имеет полюса в правой полуплоскости, то они должны совпадать с полюсами 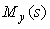 . Это обеспечивает устойчивость обратного оператора. . Это обеспечивает устойчивость обратного оператора.
В-третьих, чтобы исключить необходимость дифференцирования, порядок знаменателя 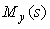 должен быть не ниже порядка знаменателя должен быть не ниже порядка знаменателя 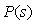 . .
Таким образом, задача синтеза регулятора с прямой связью является задачей аппроксимации нереализуемой передаточной функцией искусственно выбранной реализуемой функцией по критерию минимума погрешности.
Синтез обратного оператора удобно начинать с очевидного требования, что в установившемся режиме должно выполняться соотношение
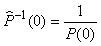 , , |
(5.64)
|
где символом 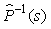 , мы обозначили оператор, который приближенно соответствует оператору , мы обозначили оператор, который приближенно соответствует оператору 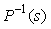 . .
Желательно, чтобы передаточная функция обратного оператора была малой на тех частотах, на которых она имеет максимальную чувствительность к изменению параметров.
Используя перечисленные требования, обратный оператор (5.63) можно аппроксимировать выражением
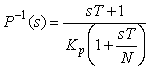 . . |
(5.65)
|
Эта передаточная функция удовлетворяет изложенным выше требованиям. Параметр 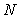 здесь определяет степень ослабления шумов дифференцирования на частотах выше здесь определяет степень ослабления шумов дифференцирования на частотах выше 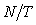 . .
Регулятор с передаточной функцией объекта
В очень простом частном случае, для систем с монотонным откликом на ступенчатое воздействие, вид передаточной функции 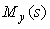 можно выбрать совпадающим с нормированной передаточной функцией объекта: можно выбрать совпадающим с нормированной передаточной функцией объекта:
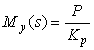 , , |
(5.66)
|
где 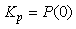 . Тогда, в соответствии с (5.62) . Тогда, в соответствии с (5.62)
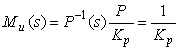 . . |
(5.67)
|
Недостатком такого подхода является медленная реакция замкнутой системы на изменение задающего воздействия. Достоинством является отсутствие каких-либо расчетов и настроек для гарантированного получения отклика без перерегулирования (рис. 5.49). Следует, однако, помнить, что отклик замкнутой системы на задающее воздействие никак не связан с откликом на внешние возмущения и шум, поэтому настройка регулятора должна быть выполнена обычными методами.
Импульсное управление без обратной связи
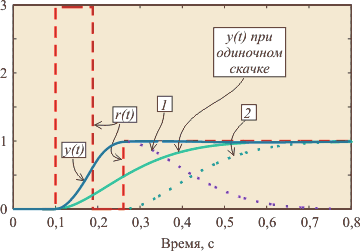
Еще одна модификация принципа разомкнутого управления состоит в том, что перед тем, как подать сигнал уставки, подают прямоугольный импульс большой амплитуды (рис. 5.50). Поскольку скорость нарастания реакции на прямоугольный импульс пропорциональна его амплитуде, длительность переходного процесса можно существенно уменьшить по сравнению со случаем, когда сигнал уставки подается в форме одиночного скачка (рис. 5.50).
Реакция на прямоугольный импульс состоит из фазы нарастания сигнала и фазы спада. Амплитуду импульса выбирают максимально возможной. Обычно она ограничивается мощностью исполнительных устройств системы. Длительность импульса выбирают такой, чтобы максимум реакции на импульс был равен значению уставки (единице при уставке в форме единичного скачка). Задержку подачи сигнала уставки выбирают так, чтобы она совпала с моментом появления максимума отклика на прямоугольный импульс.
В данном методе время выхода системы на режим может быть сделано как угодно малым, если использовать импульс достаточно большой амплитуды. В общем случае перед подачей сигнала уставки можно подавать несколько импульсов разной амплитуды и длительности. Параметры импульсов и задержку выбирают, решая численными методами задачу оптимизации, минимизируя погрешность отклонения отклика системы от требуемой формы. Для линейных систем полученные при оптимизации параметры остаются без изменений для любых значений уставки, если амплитуду прямоугольного импульса изменять пропорционально значению уставки.
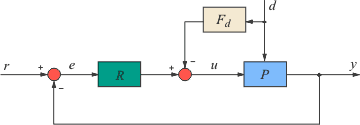
Компенсация внешних возмущений с помощью прямой связи
Если внешние возмущения, воздействующие на объект управления, можно измерять до того, как они пройдут на выход системы  , то их влияние можно существенно ослабить с помощью прямой связи. Прямая связь, в отличие от обратной, позволяет скомпенсировать погрешность быстрее, чем обратная связь обнаружит ошибку как разность между управляемой величиной и управляющим воздействием. , то их влияние можно существенно ослабить с помощью прямой связи. Прямая связь, в отличие от обратной, позволяет скомпенсировать погрешность быстрее, чем обратная связь обнаружит ошибку как разность между управляемой величиной и управляющим воздействием.
|
|
|
Рис. 5.51. Принцип компенсации возмущающих воздействий с помощью прямой связи
|
Ранее мы предполагали, что внешние возмущения приложены к входу системы. Такое допущение было справедливо при качественном анализе степени подавления возмущений с помощью обратной связи. Однако для компенсации возмущений необходимо идентифицировать передаточную функцию от точки приложения возмущений к выходу системы  . При этом объект управления приобретает второй вход - вход возмущений и описывается функцией с двумя аргументами, . При этом объект управления приобретает второй вход - вход возмущений и описывается функцией с двумя аргументами, 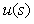 и и 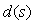 : :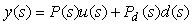 . .
Одним из вариантов компенсации члена 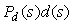 является использование принципа прямой связи (разомкнутого управления), как показано на рис. 5.51. Здесь является использование принципа прямой связи (разомкнутого управления), как показано на рис. 5.51. Здесь 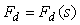 - передаточная функция регулятора с прямой связью. - передаточная функция регулятора с прямой связью.
Уравнение полученной системы можно записать непосредственно по рис. 5.51 с учетом (5.68):
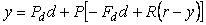 , или , или 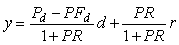 . . |
(5.69)
|
Отсюда следует, что уменьшить влияние внешних возмущений можно двумя способами: увеличивая петлевое усиление контура с обратной связью 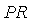 или выбрав или выбрав 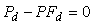 , т.е. , т.е.
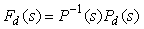 . . |
(5. 70)
|
Обращение динамического оператора здесь сопряжено с проблемами, описанными в разделе "Нахождение обратной динамики объекта". В ряде практических случаев бывает достаточно считать, что оператор 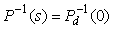 статический, что существенно упрощает его нахождение. Статические операторы используют, в частности, при компенсации влияния скорости ветра или температуры наружного воздуха для стабилизации температуры в промышленных теплицах. статический, что существенно упрощает его нахождение. Статические операторы используют, в частности, при компенсации влияния скорости ветра или температуры наружного воздуха для стабилизации температуры в промышленных теплицах.
В частном случае, когда точка приложения возмущения совпадает с входом объекта (как на рис. 5.35), (5.68) упрощается до 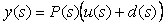 и из (5.70) получим и из (5.70) получим 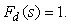
Метод прямой связи позволяет скомпенсировать возмущение до того, как оно пройдет через объект. Это существенно увеличивает общее быстродействие системы и исключает ее потенциальную неустойчивость.
Примером применения описанного метода является компенсации влияния погодных условий на промышленную теплицу. Для компенсации влияния температуры наружного воздуха, скорости ветра, осадков необходимо установить снаружи теплицы соответствующие датчики и выполнить идентификацию передаточной функции от каждого датчика до точки измерения температуры внутри теплицы, затем найти обратный оператор (5.70) и включить его в структуру регулятора.
Правильно настроенный контроллер с прямой и обратной связью позволяет ослабить влияние нагрузки на управляемую переменную до 10 раз [Techmation], www.protuner.com.
Недостатком метода является невозможность достаточно точной идентификации возмущения и точки его приложения к объекту, поскольку они распределены в пространстве, а также проблемы, связанные с нахождением обратного оператора (раздел "Принцип разомкнутого управления").
5.3.4. Регулятор отношений
Задача регулировки отношений возникает, когда важно поддерживать не абсолютные значения параметров, а соотношение между ними. Например, если решается задача смешивания компонентов в заданных пропорциях, поддерживается горение с заданным процентным содержанием кислорода в горючей смеси, и т. п.
|
|
|
|
Рис. 5.52. ПИД-регулятор отношений 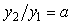
|
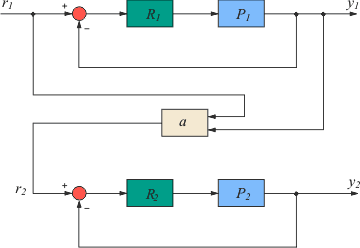
Рис. 5.53. ПИД-регулятор отношений 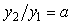 с увеличенным быстродействием с увеличенным быстродействием
|
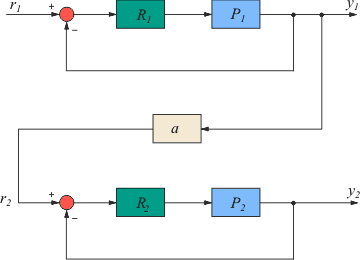
Пример решения данной задачи представлен на рис. 5.52. Первый регулятор поддерживает выходную величину 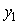 равной значению уставки равной значению уставки 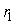 . Значение уставки второго регулятора пропорционально регулируемой величине первого регулятора: . Значение уставки второго регулятора пропорционально регулируемой величине первого регулятора: 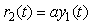 . Величина отношения устанавливается блоком . Величина отношения устанавливается блоком 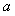 на рис. 5.52 и может изменяться в соответствии с алгоритмом работы системы. Сигнал желательно брать именно с выхода системы на рис. 5.52 и может изменяться в соответствии с алгоритмом работы системы. Сигнал желательно брать именно с выхода системы 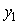 , это повышает точность, поскольку , это повышает точность, поскольку 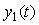 отличается от отличается от 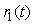 на величину погрешности, которая в динамике может быть значительной. Кроме того, величина на величину погрешности, которая в динамике может быть значительной. Кроме того, величина 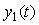 всегда изменяется с некоторой задержкой относительно всегда изменяется с некоторой задержкой относительно 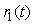 . Поэтому величина . Поэтому величина 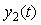 будет отставать по времени от желаемого значения будет отставать по времени от желаемого значения 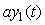 . .
Смягчить эту проблему позволяет структура, показанная на рис. 5.53. Здесь блок 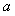 имеет два входа и описывается выражением имеет два входа и описывается выражением
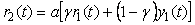 , ,
где 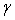 - параметр, определяющий вклад - параметр, определяющий вклад 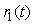 или или 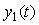 в величину в величину 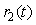 . При . При 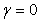 эта структура идентична структуре на рис. 5.52. эта структура идентична структуре на рис. 5.52.
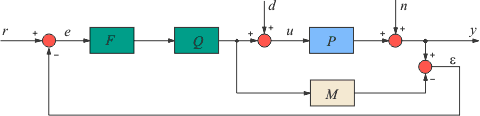
5.3.5. Регулятор с внутренней моделью
Если модель 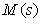 объекта объекта 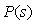 идентифицирована, то можно не рассчитывать параметры ПИД-регулятора, если использовать регулятор с показанной на рис. 5.54 структурой [Karakawa, Ho, Tamayo, Lee]. Здесь идентифицирована, то можно не рассчитывать параметры ПИД-регулятора, если использовать регулятор с показанной на рис. 5.54 структурой [Karakawa, Ho, Tamayo, Lee]. Здесь 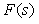 - фильтр, обычно выбираемый с передаточной функцией - фильтр, обычно выбираемый с передаточной функцией
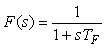 ; ; |
(5.71)
|
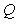 - обращенная модель объекта, т.е. - обращенная модель объекта, т.е. 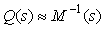 . Знак приближенного равенства стоит потому, что обращение модели редко можно выполнить точно, см. "Нахождение обратной динамики объекта". . Знак приближенного равенства стоит потому, что обращение модели редко можно выполнить точно, см. "Нахождение обратной динамики объекта".
Для описания принципа действия регулятора на рис. 5.54 предположим сначала, что возмущения  и шумы измерений и шумы измерений  отсутствуют, а модель объекта управления и обращенная модель являются точными, т.е. отсутствуют, а модель объекта управления и обращенная модель являются точными, т.е.
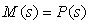 , , 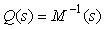 . . |
(5.72)
|
Тогда разность между сигналами на выходах процесса и модели равна нулю: 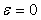 . Но в таком случае . Но в таком случае 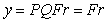 и, учитывая, что и, учитывая, что 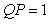 , получим , получим
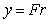 . . |
(5.73)
|
|
|
|
Рис. 5.54. Регулятор с внутренней моделью 
|
|
|
|
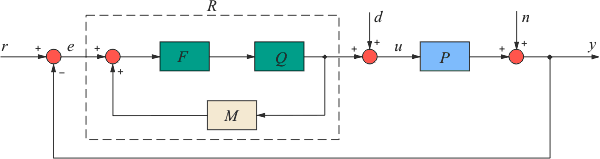
Рис. 5.55. Регулятор с внутренней моделью 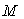 в классической форме представления (с регулятором в классической форме представления (с регулятором 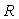 ) )
|
Поскольку в установившемся режиме 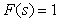 (5.71), то получим (5.71), то получим 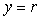 . Таким образом, регулятор с внутренней моделью точно поддерживает значение уставки в статическом режиме. . Таким образом, регулятор с внутренней моделью точно поддерживает значение уставки в статическом режиме.
Фильтр нижних частот 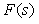 в такой структуре с помощью настройки граничной частоты в такой структуре с помощью настройки граничной частоты 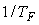 позволяет выбрать компромисс между запасом устойчивости и быстродействием замкнутой системы. позволяет выбрать компромисс между запасом устойчивости и быстродействием замкнутой системы.
Регулятор, представленный на рис. 5.54, путем переноса блока вычисления разности  может быть преобразован в классическую форму ПИД-регулятора (рис. 5.35, рис. 5.55), где может быть преобразован в классическую форму ПИД-регулятора (рис. 5.35, рис. 5.55), где
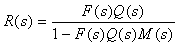 . . |
(5.74)
|
В общем случае регулятор (5.74) может иметь высокий порядок, который определяется порядком объекта. Однако в частном случае описанная структура вырождается в обычный ПИ- или ПИД-регулятор [Leva]. Предположим, что модель объекта описывается передаточной функцией
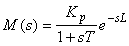 . . |
(5.75)
|
Приближенная обратная функция будет иметь следующий вид (см. раздел "Принцип разомкнутого управления"):
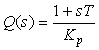 . . |
(5.76)
|
Можно уточнить вид функции (5.75), если использовать аппроксимацию задержки 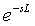 линейным членом ряда Тейлора: линейным членом ряда Тейлора:
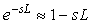 , , 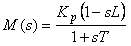 . . |
(5.77)
|
С учетом приведенных выражений для 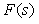 , , 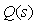 и и 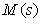 уравнение регулятора (5.74) примет вид уравнение регулятора (5.74) примет вид
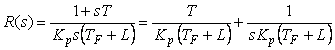 . . |
(5.78)
|
Как видим, это уравнение ПИ-регулятора, в котором пропорциональный коэффициент равен 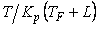 , а постоянная интегрирования - , а постоянная интегрирования - 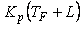 . .
ПИД-регулятор можно получить из регулятора с внутренней моделью, если задержку 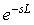 заменить аппроксимацией Паде первого порядка [Astrom]: заменить аппроксимацией Паде первого порядка [Astrom]:
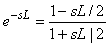 . . |
(5.79)
|
При этом уравнение (5.74) преобразуется к виду
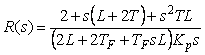 . . |
(5.80)
|
В знаменателе этого выражения для частот ниже 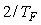 и и 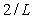 можно пренебречь членом можно пренебречь членом 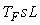 по сравнению с по сравнению с 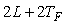 : :
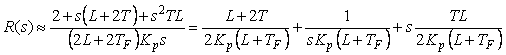 . . |
(5. 81)
|
Как видим, получилась передаточная функция классического ПИД-регулятора.
Таким образом, для объектов управления первого порядка регулятор с внутренней моделью при допущениях (5.77) и (5.81) эквивалентен ПИ- или ПИД-регулятору.
Важной особенностью регулятора с внутренней моделью является возможность настройки робастности независимо от выбора остальных параметров регулятора. Для этого выбирают соответствующий фильтр 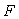 или параметр или параметр 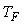 для фильтра первого порядка (5.71). Регулятор с внутренней моделью может дать очень хорошую реакцию на изменение уставки, однако реакция на внешние возмущения может быть слишком замедленной, поскольку в выражении (5.74) сокращаются нули и полюса передаточной функции, см подробнее этот эффект в разделе "Сокращение нулей и полюсов" для фильтра первого порядка (5.71). Регулятор с внутренней моделью может дать очень хорошую реакцию на изменение уставки, однако реакция на внешние возмущения может быть слишком замедленной, поскольку в выражении (5.74) сокращаются нули и полюса передаточной функции, см подробнее этот эффект в разделе "Сокращение нулей и полюсов"
Проектирование регулятора с внутренней моделью происходит следующим образом [Leva]. Сначала находят и оптимизируют обратную модель 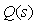 исходя из требований к качеству переходного процесса при изменении уставки, не обращая внимания на робастность. Для получения начального приближения исходя из требований к качеству переходного процесса при изменении уставки, не обращая внимания на робастность. Для получения начального приближения 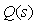 предполагают, что предполагают, что 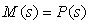 и используют методы обращения динамического оператора, описанные в разделе "Принцип разомкнутого управления". Единственным ограничением при оптимизации передаточной функции и используют методы обращения динамического оператора, описанные в разделе "Принцип разомкнутого управления". Единственным ограничением при оптимизации передаточной функции 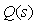 является требование ее асимптотической устойчивости. После этого выбирают структуру и параметры фильтра является требование ее асимптотической устойчивости. После этого выбирают структуру и параметры фильтра 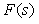 , добиваясь требуемой робастности системы при заданном быстродействии. Поскольку в идеальном случае (5.73) свойства замкнутой системы определяются характеристикой выбранного фильтра, его граничная частота в этом случае определяет быстродействие всей замкнутой системы. , добиваясь требуемой робастности системы при заданном быстродействии. Поскольку в идеальном случае (5.73) свойства замкнутой системы определяются характеристикой выбранного фильтра, его граничная частота в этом случае определяет быстродействие всей замкнутой системы.
Для объектов, у которых транспортная задержка 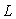 составляет менее 0,25 от доминирующей постоянной времени объекта составляет менее 0,25 от доминирующей постоянной времени объекта  , постоянную времени фильтра приближенно можно выбрать из диапазона от , постоянную времени фильтра приближенно можно выбрать из диапазона от 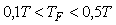 [Leva]. Если [Leva]. Если 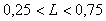 , то , то  . Если транспортная задержка еще больше, то постоянную времени фильтра еще более увеличивают, выбирая в качестве начального приближения . Если транспортная задержка еще больше, то постоянную времени фильтра еще более увеличивают, выбирая в качестве начального приближения 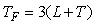 [Leva]. [Leva].
|
|
|
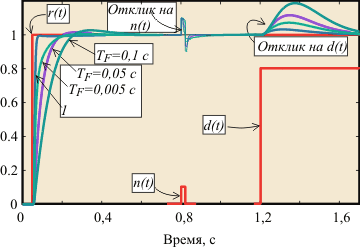
Рис. 5.56. Реакция системы со встроенной моделью на входной импульс, помеху и возмущение для разных параметров фильтра 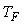 ; 1 - модель точно соответствует объекту и ; 1 - модель точно соответствует объекту и 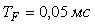
|
Пример реакции системы со встроенной моделью на изменение уставки 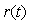 , на импульс помехи , на импульс помехи 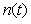 и возмущение и возмущение 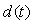 приведен на рис. 5.56. Объект описывается передаточной функцией вида приведен на рис. 5.56. Объект описывается передаточной функцией вида 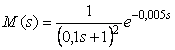 . Модель описывается передаточной функцией . Модель описывается передаточной функцией 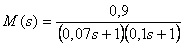 , т.е. модель не точно соответствует объекту. Обратный оператор , т.е. модель не точно соответствует объекту. Обратный оператор 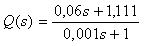 . Отметим, что для обеспечения точности в установившемся режиме должно выполняться соотношение . Отметим, что для обеспечения точности в установившемся режиме должно выполняться соотношение 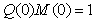 , поскольку коэффициент передачи регулятора в установившемся режиме должен стремиться к бесконечности (см. (5.74)). На рис. 5.56 кривая 1 соответствует случаю, когда модель точно соответствует объекту, а постоянная времени фильтра , поскольку коэффициент передачи регулятора в установившемся режиме должен стремиться к бесконечности (см. (5.74)). На рис. 5.56 кривая 1 соответствует случаю, когда модель точно соответствует объекту, а постоянная времени фильтра 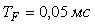 . Как видим, повышение точности модели и уменьшение постоянной времени фильтра позволяют существенно увеличить быстродействие системы, однако реакция на возмущающие воздействия при этом изменяется слабо. . Как видим, повышение точности модели и уменьшение постоянной времени фильтра позволяют существенно увеличить быстродействие системы, однако реакция на возмущающие воздействия при этом изменяется слабо.
5.3.6. Эквивалентные преобразования структур ПИД-регуляторов
В литературе описано много различных структур ПИД-регуляторов, однако многие из них эквивалентны между собой и могут быть преобразованы одна в другую. Эквивалентность в данном случае понимается в том смысле, что уравнения, записанные для одной структуры, идентичны уравнениям другой структуры.
Рассмотрим два фрагмента структурных схем, показанные на рис. 5.57-а и -б. Первый фрагмент описывается выражением 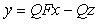 , второй - выражением , второй - выражением 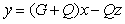 . Сравнивая эти выражения между собой, получим условие их эквивалентности: . Сравнивая эти выражения между собой, получим условие их эквивалентности: 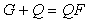 , или , или
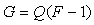 . . |
(5.82)
|
На рис. 5.58 показана типовая структурная реализация интегрального члена в промышленных ПИД-регуляторах [Astrom]. Непосредственно по структурной схеме можно записать уравнение
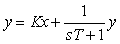 , из которого можно найти , из которого можно найти
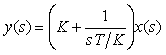 . . |
(5.83)
|
 |
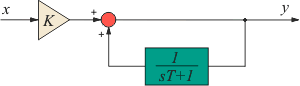 |
Рис. 5.57. Две эквивалентные структурные схемы |
Рис. 5.58. Структура ПИ-регулятора
|
Таким образом, структура на рис. 5.58 описывает ПИ-регулятор с постоянной интегрирования 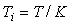 . Такой способ получения интегрального и пропорционального члена использовался еще в аналоговых регуляторах. Он был хорош тем, что передаточная функция . Такой способ получения интегрального и пропорционального члена использовался еще в аналоговых регуляторах. Он был хорош тем, что передаточная функция 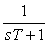 была легко технически реализуема с помощью интегрирующей RC-цепочки, состоящей из одного резистора и одного конденсатора. Несмотря на то, что в современных регуляторах RC-цепочки не используются, этот способ до сих пор применяется в серийных промышленных регуляторах [Astrom]. была легко технически реализуема с помощью интегрирующей RC-цепочки, состоящей из одного резистора и одного конденсатора. Несмотря на то, что в современных регуляторах RC-цепочки не используются, этот способ до сих пор применяется в серийных промышленных регуляторах [Astrom].
Кроме классического уравнения ПИД-регулятора (5.40), получила распространение эквивалентная ей так называемая последовательная форма ПИД-регулятора , передаточная функция которой имеет вид
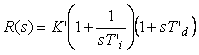 . . |
(5.84)
|
Раскрывая скобки в (5.84), получим 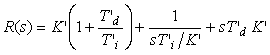 , т. е. последовательная форма ПИД-регулятора эквивалентна обычной, если обозначить , т. е. последовательная форма ПИД-регулятора эквивалентна обычной, если обозначить 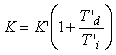 , , 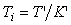 , , 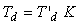 . .
5.3.7. ПИД-регуляторы для систем с транспортной задержкой
|
|
|
|
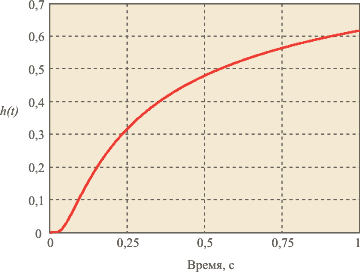
Рис. 5.59. Переходная характеристика пространственно протяженного теплового объекта
|
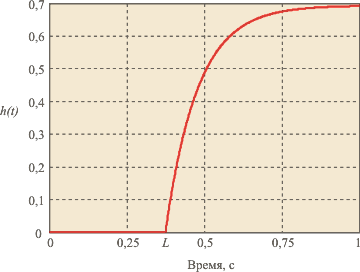
Рис. 5.60. Переходная характеристика объекта с транспортной задержкой
|
Типовая переходная характеристика объекта управления, в котором происходит перенос тепла, показана на рис. 5.1 - рис. 5.5, рис. 5.59. Все кривые начинаются с задержки 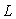 , затем происходит плавное нарастание температуры. Решение одномерного уравнения переноса тепла в бесконечно длинном теле при единичном ступенчатом воздействии температуры в точке с координатой , затем происходит плавное нарастание температуры. Решение одномерного уравнения переноса тепла в бесконечно длинном теле при единичном ступенчатом воздействии температуры в точке с координатой 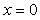 описывается функцией описывается функцией
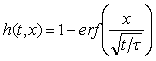
(рис. 5.59), где 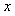 - расстояние точки измерения температуры от точки воздействия температуры, - расстояние точки измерения температуры от точки воздействия температуры, 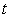 - время, - время, 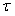 - константа. При фиксированном - константа. При фиксированном 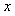 это уравнение можно преобразовать к виду это уравнение можно преобразовать к виду  , где , где 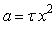 - константа. Таким образом, расстояние от точки приложения температуры до точки ее измерения влияет только на масштаб по времени, в котором изображена переходная характеристика объекта, но не на соотношение между длительностью задержки и длительностью переходного процесса. Иначе говоря, соотношение между задержкой и длительностью переходного процесса практически не зависит от размеров теплового объекта. С увеличением размеров объекта растет транспортная задержка, но одновременно растет и длительность переходного процесса. - константа. Таким образом, расстояние от точки приложения температуры до точки ее измерения влияет только на масштаб по времени, в котором изображена переходная характеристика объекта, но не на соотношение между длительностью задержки и длительностью переходного процесса. Иначе говоря, соотношение между задержкой и длительностью переходного процесса практически не зависит от размеров теплового объекта. С увеличением размеров объекта растет транспортная задержка, но одновременно растет и длительность переходного процесса.
Существуют, однако, объекты, в которых транспортная задержка может быть как угодно большой по сравнению с длительностью переходного процесса (рис. 5.60). Примером могут служить процессы, связанные с перемещением тел в пространстве, например, транспортировка по трубам и транспортерным лентам.
Поскольку у звена с транспортной задержкой сдвиг фаз 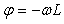 увеличивается с ростом задержки увеличивается с ростом задержки 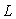 , а частота , а частота 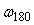 увеличивается с уменьшением длительности переходного процесса увеличивается с уменьшением длительности переходного процесса 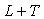 , то отношение , то отношение 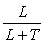 характеризует степень сложности управления объектом. характеризует степень сложности управления объектом.
Предиктор Смита
|
|
|
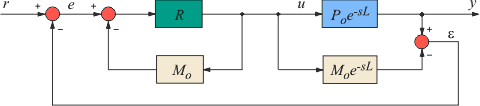
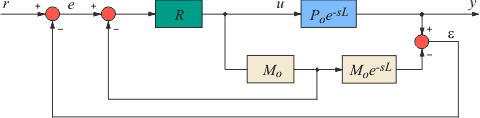
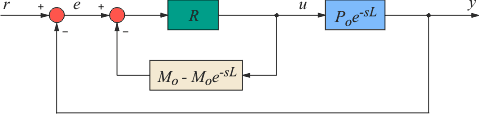
Рис. 5.61. Система управления с предиктором Смита
|
Для управления объектами с большой транспортной задержкой, обычно при 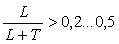 , используют специальные структуры ПИД-регуляторов, содержащие блоки для предсказания поведения объекта через время , используют специальные структуры ПИД-регуляторов, содержащие блоки для предсказания поведения объекта через время 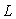 - предикторы (от английского "prediction"). На рис. 5.61 показана структура такого регулятора, предложенная Смитом в 1957 году [Smith] и иногда называемая предиктором Смита. Предиктор Смита включен в некоторые промышленные ПИД-регуляторы. - предикторы (от английского "prediction"). На рис. 5.61 показана структура такого регулятора, предложенная Смитом в 1957 году [Smith] и иногда называемая предиктором Смита. Предиктор Смита включен в некоторые промышленные ПИД-регуляторы.
Цель предиктора Смита - предсказать, какой сигнал появится на выходе объекта до того, как он там появится на самом деле. Для предсказания можно использовать модель объекта управления, состоящую из дробно-рациональной части 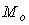 и транспортной задержки и транспортной задержки 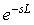 (рис. 5.61). Благодаря тому, что из модели можно исключить задержку, появляется принципиальная возможность предсказания поведения объекта до появления сигнала на его выходе. (рис. 5.61). Благодаря тому, что из модели можно исключить задержку, появляется принципиальная возможность предсказания поведения объекта до появления сигнала на его выходе.
Реализуется эта возможность системой со структурой, показанной на (рис. 5.61). Здесь - 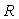 - обычный ПИД-регулятор, - обычный ПИД-регулятор, 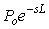 - передаточная характеристика объекта управления. - передаточная характеристика объекта управления.
|
|
|
Рис. 5.62. Одна из модификаций системы управления с предиктором Смита
|
Принцип работы системы состоит в следующем. Предположим, что модель абсолютна точна. Тогда разность сигналов на выходах модели и объекта будет равна нулю, 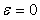 . Но в таком случае непосредственно из (рис. 5.61) можно получить . Но в таком случае непосредственно из (рис. 5.61) можно получить 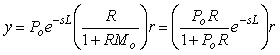 . В этом выражении член . В этом выражении член 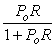 представляет собой передаточную функцию системы без транспортной задержки (сравните ее с (5.41)). А это значит, что звено с транспортной задержкой не входит в контур обратной связи и не влияет на устойчивость и быстродействие системы, т.е. происходит регулирование в контуре с моделью без задержки, а транспортная задержка только добавляется к полученному результату. представляет собой передаточную функцию системы без транспортной задержки (сравните ее с (5.41)). А это значит, что звено с транспортной задержкой не входит в контур обратной связи и не влияет на устойчивость и быстродействие системы, т.е. происходит регулирование в контуре с моделью без задержки, а транспортная задержка только добавляется к полученному результату.
Рассмотрим теперь работу предиктора Смита без предположения 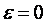 . В этом случае рис. 5.61 можно описать следующей системой уравнений: . В этом случае рис. 5.61 можно описать следующей системой уравнений:
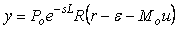 , , 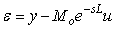 , , 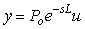 , ,
откуда можно найти
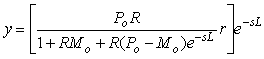 . . |
(5.85)
|
|
|
|
Рис. 5.63. Вторая модификация системы управления с предиктором Смита
|
Как видим, с ростом точности модели разность 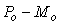 в знаменателе стремится к нулю и из передаточной функции системы исключается транспортная задержка, которая только добавляется к уже полученному результату регулирования (в квадратных скобках (5.85)). в знаменателе стремится к нулю и из передаточной функции системы исключается транспортная задержка, которая только добавляется к уже полученному результату регулирования (в квадратных скобках (5.85)).
С помощью топологических преобразований структурных схем можно получить много эквивалентных между собой структур систем с предиктором Смита. Две из них представлены на рис. 5.62 и рис. 5.63. Можно показать, что они описываются тем же уравнением (5.85).
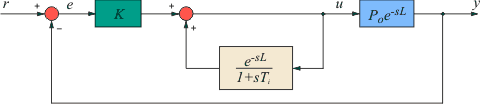
ППИ-регуляторы
ППИ-регулятор (сокращение от "Предиктивный ПИ" - "предсказывающий") является модификацией предиктора Смита, которая распространена в АСУ ТП более широко, чем сам предиктор Смита. Один из вариантов ППИ-регулятора представлен на рис. 5.64 [Leva]. Сравнивая этот рисунок с рис. 5.58, можно заметить, что ППИ регулятор отличается от обычного ПИ-регулятора только тем, что вместо единицы в числителе выражения 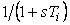 стоит изображение задержки стоит изображение задержки 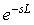 . Существует много модификаций структуры, изображенной на рис. 5.64, см., например [Astrom]. . Существует много модификаций структуры, изображенной на рис. 5.64, см., например [Astrom].
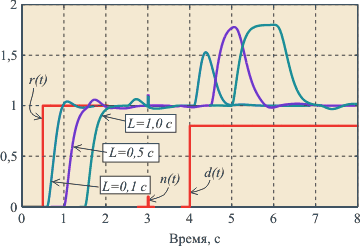
На рис. 5.65 приведена реакция системы на скачок сигнала уставки. Отметим, что ППИ-регулятор и предиктор Смита выполняют только слежение за уставкой, но очень плохо ослабляют внешние возмущения (рис. 5.65).
|
|
|
Рис. 5.64. Система управления с ППИ-регушятором
|
|
|
|
Рис. 5.65. Переходный процесс в системе с ППИ-регулятором и объектом вида (5.50) при 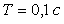 , , 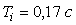 ; обозначения соответствуют рис. 5.44 ; обозначения соответствуют рис. 5.44
|
|

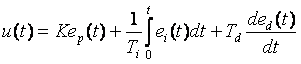
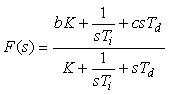 .
.
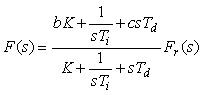 ,
,


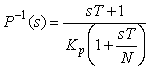 .
.



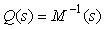 .
.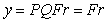 и, учитывая, что
и, учитывая, что 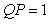 , получим
, получим


















